
小明在一次数学兴趣小组活动中,对一个数学问题作如下探究:
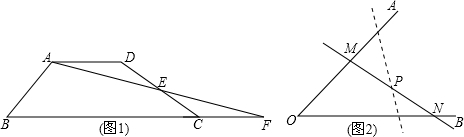
问题情境:如图1,四边形ABCD中,AD∥BC,点E为DC边的中点,连结AE并延长交BC的延长线于点F.求证:S四边形ABCD=S△ABF.(S表示面积)

问题迁移:如图2,在已知锐角∠AOB内有一定点P.过点P任意作一条直线MN,分别交射线OA、OB于点M、N.小明将直线MN绕着点P旋转的过程中发现,△MON的面积存在最小值.请问当直线MN在什么位置时,△MON的面积最小,并说明理由.

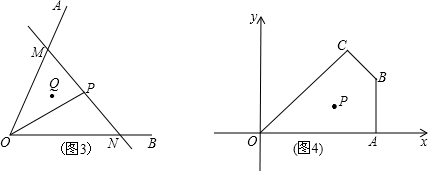
实际应用:如图3,若在道路OA、OB之间有一村庄Q发生疫情,防疫部分计划以公路OA、OB和经过防疫站的一条直线MN为隔离线,建立一个面积最小的三角形隔离区△MON.若测得∠AOB=66º,∠POB=30º,OP=4km,试求△MON的面积.(结果精确到0.1km2)(参考数据:sin66º≈0.91,tan66º≈2.25,![]() ≈1.73)
≈1.73)
拓展延伸:如图4,在平面直角坐标系中,O为坐标原点,点A、B、C、P的坐标分别为(6,0)、(6,3)、![]() 、(4,2),过点P的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形的面积的最大值.
、(4,2),过点P的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形的面积的最大值.
问题情境:根据已知可以求得△ADE≌△FCE,就可以得出S△ADE=S△FCE,从而得出结论。
问题迁移:根据问题情境的结论可以得出当直线旋转到点P是MN的中点时S△MON最小,过点M作MG∥OB交EF于G.由全等三角形的性质可以得出结论。
实际运用:∴![]() 。
。
拓展延伸:截得四边形面积的最大值为10
【解析】
分析:问题情境:根据已知可以求得△ADE≌△FCE,就可以得出S△ADE=S△FCE,从而得出结论。
问题迁移:根据问题情境的结论可以得出当直线旋转到点P是MN的中点时S△MON最小,过点M作MG∥OB交EF于G.由全等三角形的性质可以得出结论。
实际运用:如图3,作PP1⊥OB,MM1⊥OB,垂足分别为P1,M1,再根据条件由三角函数值就可以求出结论。
拓展延伸:分情况讨论当过点P的直线l与四边形OABC的一组对边OC、AB分别交于点M、N,延长OC、AB交于点D,由条件可以得出AD=6,就可以求出△OAD的面积,再根据问题迁移的结论就可以求出最大值;
当过点P的直线l与四边形OABC的另一组对边CB、OA分别交M、N,延长CB交x轴于T,由B、C的坐标可得直线BC的解析式,就可以求出T的坐标,从而求出△OCT的面积,再由问题迁移的结论可以求出最大值,通过比较即可以求出结论。
解:问题情境:证明:∵AD∥BC,∴∠DAE=∠F,∠D=∠FCE。
∵点E为DC边的中点,∴DE=CE。
∵在△ADE和△FCE中, ,
,
∴△ADE≌△FCE(AAS)。∴S△ADE=S△FCE。
∴S四边形ABCE+S△ADE=S四边形ABCE+S△FCE,即S四边形ABCD=S△ABF。
问题迁移:当直线旋转到点P是MN的中点时S△MON最小,理由如下:
如图2,过点P的另一条直线EF交OA、OB于点E、F,

设PF<PE,过点M作MG∥OB交EF于G,
由问题情境可以得出当P是MN的中点时S四边形MOFG=S△MON。
∵S四边形MOFG<S△EOF,∴S△MON<S△EOF。
∴当点P是MN的中点时S△MON最小。
实际运用:如图3,作PP1⊥OB,MM1⊥OB,垂足分别为P1,M1,
在Rt△OPP1中,∵∠POB=30°,

∴PP1=![]() OP=2,OP1=2
OP=2,OP1=2![]() 。
。
由问题迁移的结论知,当PM=PN时,△MON的面积最小,
∴MM1=2PP1=4,M1P1=P1N。
在Rt△OMM1中,![]() ,即
,即![]() ,
,
∴![]() 。∴
。∴![]() 。
。
∴![]() 。
。
∴![]() 。
。
拓展延伸:①如图4,当过点P的直线l与四边形OABC的一组对边OC、AB分别交于点M、N,延长OC、AB交于点D,

∵C![]() ,∴∠AOC=45°。∴AO=AD。
,∴∠AOC=45°。∴AO=AD。
∵A(6,0),∴OA=6。∴AD=6。
∴![]() 。
。
由问题迁移的结论可知,当PN=PM时,△MND的面积最小,
∴四边形ANMO的面积最大。
作PP1⊥OA,MM1⊥OA,垂足分别为P1,M1,
∴M1P1=P1A=2。∴OM1=M1M=2,∴MN∥OA。
∴![]() 。
。
②如图5,当过点P的直线l与四边形OABC的另一组对边CB、OA分别交M、N,延长CB交x轴于T,
设直线BC的解析式为y=kx+b,

∵C![]() 、B(6,3),
、B(6,3),
∴ ,解得:
,解得:![]() 。
。
∴直线BC的解析式为![]() 。
。
当y=0时,x=9,∴T(9,0)。
∴![]() 。
。
由问题迁移的结论可知,当PM=PN时,△MNT的面积最小,
∴四边形CMNO的面积最大。
∴NP1=M1P1,MM1=2PP1=4。∴![]() ,解得x=5。∴M(5,4)。
,解得x=5。∴M(5,4)。
∴OM1=5。
∵P(4,2),∴OP1=4。∴P1M1=NP1=1。∴ON=3。∴NT=6。
∴![]() 。
。
∴![]() 。
。
∴综上所述:截得四边形面积的最大值为10。


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
| 3 |
| 9 |
| 2 |
| 9 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(江苏连云港卷)数学(带解析) 题型:解答题
小明在一次数学兴趣小组活动中,对一个数学问题作如下探究:
问题情境:如图1,四边形ABCD中,AD∥BC,点E为DC边的中点,连结AE并延长交BC的延长线于点F.求证:S四边形ABCD=S△ABF.(S表示面积)
问题迁移:如图2,在已知锐角∠AOB内有一定点P.过点P任意作一条直线MN,分别交射线OA、OB于点M、N.小明将直线MN绕着点P旋转的过程中发现,△MON的面积存在最小值.请问当直线MN在什么位置时,△MON的面积最小,并说明理由.
实际应用:如图3,若在道路OA、OB之间有一村庄Q发生疫情,防疫部分计划以公路OA、OB和经过防疫站的一条直线MN为隔离线,建立一个面积最小的三角形隔离区△MON.若测得∠AOB=66º,∠POB=30º,OP=4km,试求△MON的面积.(结果精确到0.1km2)(参考数据:sin66º≈0.91,tan66º≈2.25, ≈1.73)
≈1.73)
拓展延伸:如图4,在平面直角坐标系中,O为坐标原点,点A、B、C、P的坐标分别为(6,0)、(6,3)、 、(4,2),过点P的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形的面积的最大值.
、(4,2),过点P的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形的面积的最大值.
查看答案和解析>>
科目:初中数学 来源:2013年江苏省连云港市中考数学试卷(解析版) 题型:解答题


 ≈1.73)
≈1.73) ,
, )、(4、2),过点p的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形面积的最大值.
)、(4、2),过点p的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形面积的最大值.查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(江苏连云港卷)数学(解析版) 题型:解答题
小明在一次数学兴趣小组活动中,对一个数学问题作如下探究:
问题情境:如图1,四边形ABCD中,AD∥BC,点E为DC边的中点,连结AE并延长交BC的延长线于点F.求证:S四边形ABCD=S△ABF.(S表示面积)

问题迁移:如图2,在已知锐角∠AOB内有一定点P.过点P任意作一条直线MN,分别交射线OA、OB于点M、N.小明将直线MN绕着点P旋转的过程中发现,△MON的面积存在最小值.请问当直线MN在什么位置时,△MON的面积最小,并说明理由.

实际应用:如图3,若在道路OA、OB之间有一村庄Q发生疫情,防疫部分计划以公路OA、OB和经过防疫站的一条直线MN为隔离线,建立一个面积最小的三角形隔离区△MON.若测得∠AOB=66º,∠POB=30º,OP=4km,试求△MON的面积.(结果精确到0.1km2)(参考数据:sin66º≈0.91,tan66º≈2.25, ≈1.73)
≈1.73)
拓展延伸:如图4,在平面直角坐标系中,O为坐标原点,点A、B、C、P的坐标分别为(6,0)、(6,3)、 、(4,2),过点P的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形的面积的最大值.
、(4,2),过点P的直线l与四边形OABC一组对边相交,将四边形OABC分成两个四边形,求其中以点O为顶点的四边形的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com