
如图,AP∥BC, PAB的平分线与
PAB的平分线与 CBA的平分线相交于E,CE的延长线交AP于D,
CBA的平分线相交于E,CE的延长线交AP于D,
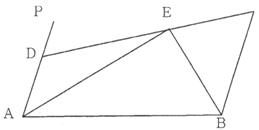
求证:(1)AB=AD+BC(2)若BE=3,AE=4,求四边形ABCD的面积?
(1)证明见解析(2)12
【解析】延长AE交BC延长线于M
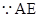 平分
平分 ,BE平分
,BE平分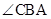
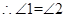 ,
, 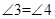
 AD//BC
AD//BC
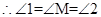 ,
, 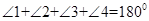
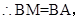
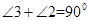

 在
在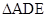 和
和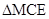 中
中
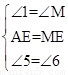

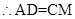
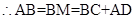
②由①知: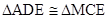
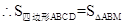
又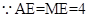 , BE=3
, BE=3
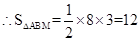
(1)通过构造全等三角形来求解,延长AE交BC的延长线于M;由AP∥BC,及AE平分∠PAB,可求得∠BAE=∠M,即AB=BM,因此直线证得AD=MC即可;在等腰△ABM中,BE是顶角的平分线,根据等腰三角形三线合一的性质知:E是AM的中点,即AE=EM,而PA∥BM,即可证得△ADE≌△MCE,从而得到所求的结论.
(2)由(1)的全等三角形可知:△ADE、△MCE的面积相等,从而将所求四边形的面积转化为等腰△ABM的面积,易得AM、BE的值,从而根据三角形的面积公式求得△ABM的面积,即四边形ADCB的面积.


科目:初中数学 来源: 题型:
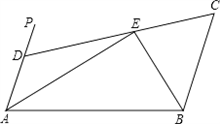
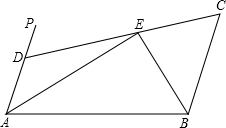 如图,AP∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的延长线交AP于D.
如图,AP∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的延长线交AP于D.查看答案和解析>>
科目:初中数学 来源:2011—2012学年四川成都龙泉柏合学校七年级下学期期末考试数学试卷(带解析) 题型:解答题
如图,AP∥BC,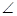 PAB的平分线与
PAB的平分线与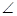 CBA的平分线相交于E,CE的延长线交AP于D,
CBA的平分线相交于E,CE的延长线交AP于D,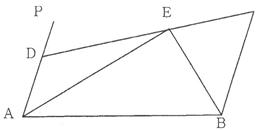
求证:(1)AB=AD+BC(2)若BE=3,AE=4,求四边形ABCD的面积?
查看答案和解析>>
科目:初中数学 来源:广东省期末题 题型:解答题
查看答案和解析>>
科目:初中数学 来源:期末题 题型:解答题
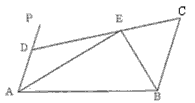
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com