
��ͼ���ڡ�ABC�У���B=45�㣬BC=5����AD=4������EFPQ��һ��QP��BC���ϣ�E��F�ֱ���AB��AC�ϣ�AD��EF�ڵ�H��
��1����֤�� ��
��
��2����EF=x����xΪ��ֵʱ������EFPQ�������������������
��3��������EFPQ��������ʱ���þ���EFPQ��ÿ��1����λ���ٶ�������DA���������˶��������εı�PQ����A��ʱֹͣ�˶��������˶�ʱ��Ϊt�룬����EFPQ���ABC�ص����ֵ����ΪS����S��t�ĺ�����ϵʽ����д��t��ȡֵ��Χ��
�⣺��1��֤�����߾���EFPQ����EF��BC��
���AHF�ס�ADC����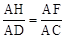 ��
��
��EF��BC�����AEF�ס�ABC����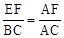 .
.
�� ��
��
��2���ߡ�B=45�㣬��BD=AD=4����CD=BC��BD=5��4=1��
��EF��BC�����AEH�ס�ABD���� ��
��
��EF��BC�����AFH�ס�ACD���� ��
��
�� ����
���� ����EH=4HF��
����EH=4HF��
��֪EF=x����EH= ��
��
�ߡ�B=45�㣬��EQ=BQ=BD��QD=BD��EH=4�� ��
�� ��
��
�൱x= ʱ������EFPQ��������������Ϊ5��
ʱ������EFPQ��������������Ϊ5��
��3���ɣ�2����֪��������EFPQ��������ʱ�����εij�Ϊ ����Ϊ
����Ϊ ��
��
�ھ���EFPQ������AD���˶������У�
��I����0��t��2ʱ�����ͼ����ʾ��
�������AB��AC�ֱ��ڵ�K��N����AD�ֱ��ڵ�H1��D1����ʱDD1=t��H1D1=2��
��HD1=HD��DD1=2��t��HH1=H1D1��HD1=t��AH1=AH��HH1=2��t��
��KN��EF���� ����
����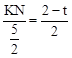 ��
��
���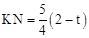 ��
�� ��
��
��II����2��t��4ʱ�����ͼ����ʾ��
�������AB��AC�ֱ��ڵ�K��N����AD���ڵ�D2����ʱDD2=t��AD2=AD��DD2=4��t��
��KN��EF���� ����
���� ��
��
��� ��
�� ��
��
����������S��t�ĺ�����ϵʽΪ��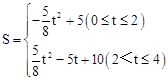 ��
��
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����ABC��һ��������������ϣ���BC=120mm����AD=80mm��Ҫ�����ӹ��������������ʹ�����ε�һ����BC�ϣ�������������ֱ���AB��AC�ϣ��������������ı߳��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��̽�����֡�
��ͼ�з�ʽ����С��ͬ�����������η���һ�𣬷ֱ������Ӱ���֣��SACF�������������λ�����ף���Ӱ���ֵ����������S1��S2��S3��ʾ��
1.S1= cm2; S2= cm2; S3= cm2.
2.�����ܽ���ķ��֣�
��������˼��
��ͼ�з�ʽ����С��ͬ�����������η���һ����С�����εı߳���bcm���������εı߳���acm������Ӱ���֣��SACF���������
��Ӧ����չ��
1.����ͼ��ʽ����С��ͬ�����������η���һ�����������ε������80cm2,��ͼ����Ӱ�����ε������ cm2.
2.��ͼ��1����C���߶�AB������һ�㣬�ֱ���AC��BCΪ�����߶�ABͬ���ȱ������ΨSACD�͵ȱ������ΨSCBE�����SCBE�ı߳���1cm����ͼ����Ӱ�����ε������ cm2.
3.��ͼ��2��������ABCD������ECGF�ı߳��ֱ�Ϊ2��3����A=120�㣬��ͼ����Ӱ���ֵ������ 

��1�� ��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
һ�����ϣ��������������õƹ��µ�Ӱ��������һ·��D�ĸ߶ȣ���ͼ���������ߵ���A��ʱ�������������ֱ������AM����Ӱ�ӳ�AE������ȣ�����������AC���������ǰ�ߣ��ߵ���B��ʱ������ֱ��ʱ����BN��Ӱ��ǡ�����߶�AB�������AB=1.25m����֪����ֱ��ʱ������Ϊ1.75m����·�Ƶĸ�CD�ij�.�������ȷ��0.1m��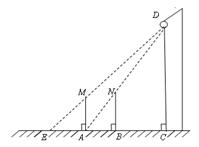
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ���ı���ABCD�У�ACƽ�֡�DAB����ADC=��ACB=90�㣬EΪAB���е㣬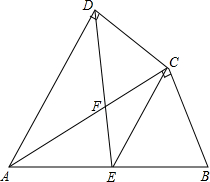
��1����֤��AC2=AB•AD��
��2����֤��CE��AD��
��3����AD=4��AB=6����  ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ����������ABCD�У��Խ���AC��BD�ཻ�ڵ�O����E��BC�ϵ�һ�����㣬����DE����AC�ڵ�F��
��1����ͼ�٣��� ʱ����
ʱ����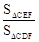 ��ֵ��
��ֵ��
��2����ͼ�ڵ�DEƽ�֡�CDBʱ����֤��AF=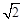 OA��
OA��
��3����ͼ�ۣ�����E��BC���е�ʱ������F��FG��BC�ڵ�G����֤��CG= BG��
BG��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��2013���Ĵ�����12�֣���ͼ����֪����OABC�У�OA=2��AB=4��˫���� ��k��0�����������AB��BC�ֱ���E��F��
��k��0�����������AB��BC�ֱ���E��F��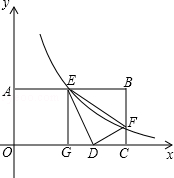
��1����E��AB���е㣬��F������ꣻ
��2��������BEF��ֱ��EF���ۣ�B������x���ϵ�D�㣬��EG��OC������ΪG��֤����EGD�ס�DCF������k��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com