
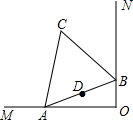
 如图,∠MON=90°,边长为2的等边三角形ABC在∠MON内部,但两顶点A、B分别在边OM、ON上滑动,点D是AB边中点
如图,∠MON=90°,边长为2的等边三角形ABC在∠MON内部,但两顶点A、B分别在边OM、ON上滑动,点D是AB边中点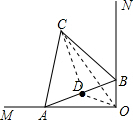 解:(1)如图,连接CD.
解:(1)如图,连接CD.| 1 |
| 2 |
| BC2-BD2 |
| 22-12 |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |


科目:初中数学 来源: 题型:
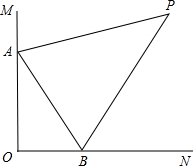 如图,∠MON=90°,AP平分∠MAB,BP平分∠ABN.
如图,∠MON=90°,AP平分∠MAB,BP平分∠ABN.查看答案和解析>>
科目:初中数学 来源: 题型:
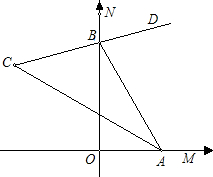 如图,∠MON=90°,点A、B分别在射线OM、ON上移动,BD是∠NBA的平分线,BD的反向延长线与∠BAO的平分线相交于点C.试猜想:∠ACB的大小是否随A、B的移动发生变化?如果保持不变,请给出证明;如果随点A、B的移动发生变化,请给出变化范围.
如图,∠MON=90°,点A、B分别在射线OM、ON上移动,BD是∠NBA的平分线,BD的反向延长线与∠BAO的平分线相交于点C.试猜想:∠ACB的大小是否随A、B的移动发生变化?如果保持不变,请给出证明;如果随点A、B的移动发生变化,请给出变化范围.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为
如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
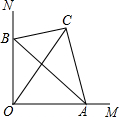 如图,∠MON=90°,△ABC的顶点A、B分别在OM、ON上,当A点从O点出发沿着OM向右运动时,同时点B在ON上运动,连结OC.若AC=4,BC=3,AB=5,则OC的长度的最大值是
如图,∠MON=90°,△ABC的顶点A、B分别在OM、ON上,当A点从O点出发沿着OM向右运动时,同时点B在ON上运动,连结OC.若AC=4,BC=3,AB=5,则OC的长度的最大值是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com