
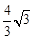 或
或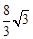 。
。

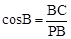 ,即
,即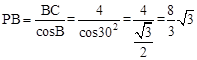 。
。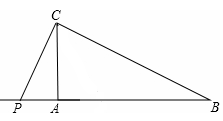
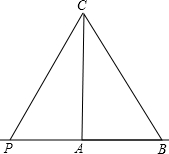
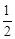 BC=2。
BC=2。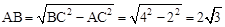 ,
,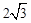 -PB。
-PB。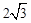 -PB)2=BP2,
-PB)2=BP2,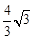 。
。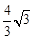 或
或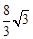 。
。

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
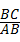 .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题: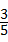 ,其中∠A为锐角,试求sadA的值.
,其中∠A为锐角,试求sadA的值.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
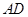 ∥
∥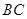 ,坝高10m,迎水坡面
,坝高10m,迎水坡面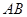 的坡度
的坡度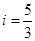 ,审核组专家看后,从力学的角度对此方案提出了建议,李设计师决定在原方案的基础上,将迎水坡面
,审核组专家看后,从力学的角度对此方案提出了建议,李设计师决定在原方案的基础上,将迎水坡面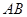 的坡度进行修改,修改后的迎水坡面
的坡度进行修改,修改后的迎水坡面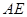 的坡度
的坡度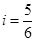 .
.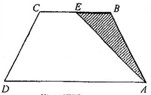
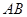 的长(结果保留根号)
的长(结果保留根号)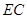 方向拓宽
方向拓宽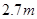 ,求坝底将会沿
,求坝底将会沿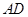 方向加宽多少米?
方向加宽多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com