
【题目】(本题12分)如图①所示,直线L: ![]() 与
与![]() 轴负半轴、
轴负半轴、![]() 轴正半轴分别交于A、B两点。
轴正半轴分别交于A、B两点。
(1)当OA=OB时,试确定直线L的解析式;
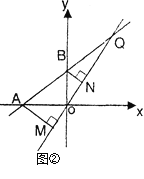
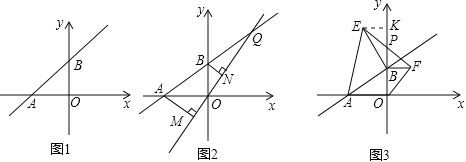
(2)在(1)的条件下,如图②所示,设Q为AB延长线上一点,作直线OQ,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,试说明MN=AM+BN。
(3)当![]() 取不同的值时,点B在
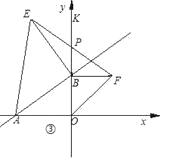
取不同的值时,点B在![]() 轴正半轴上运动,分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE,连EF交
轴正半轴上运动,分别以OB、AB为边,点B为直角顶点在第一、二象限内作等腰直角△OBF和等腰直角△ABE,连EF交![]() 轴于P点,如图③。
轴于P点,如图③。
问:当点B在 y轴正半轴上运动时,试猜想PB的长是否为定值,若是,请求出其值,若不是,说明理由。
【答案】(1)y="x+5" (2)7 (3)![]()
【解析】试题分析:(1)由直线L解析式,求出A与B坐标,根据OA=OB,求出m的值,即可确定出直线L解析式;
(2)由OA=OB,对顶角相等,且一对直角相等,利用AAS得到△AMO≌△ONB,用对应线段相等求长度;
(3)如图,作EK⊥y轴于K点,利用AAS得到△AOB≌△BKE,利用全等三角形对应边相等得到OA=BK,EK=OB,再利用AAS得到△PBF≌△PKE,寻找相等线段,并进行转化,求PB的长.
试题解析:解:(1)∵直线L:y=mx+5m,
∴A(-5,0),B(0,5m),
由OA=OB,
得5m=5,m=1,
∴直线解析式为:y=x+5;
(2)在△AMO和△OBN中,
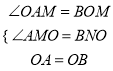 ,
,
∴△AMO≌△ONB(AAS),
∴AM=ON=4,
∴BN=OM=3,
则MN=OM+ON=4+3=7;
(3)如图,作EK⊥y轴于K点,
∵△ABE为等腰直角三角形,
∴AB=BE,∠ABE=90°,
∴∠EBK+∠ABO=90°,
∵∠EBK+∠BEK=90°,
∴∠ABO=∠BEK,
在△AOB和△BKE中,
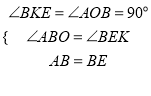 ,
,
∴△AOB≌△BKE(AAS),
∴OA=BK,EK=OB,
∵△OBF为等腰直角三角形,
∴OB=BF,
∴EK=BF,
在△EKP和△FBP中,
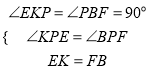 ,
,
∴△PBF≌△PKE(AAS),
∴PK=PB,
∴PB=![]() BK=
BK=![]() OA=
OA=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知一个三角形的第一条边长为2a+5b,第二条边比第一条边长3a﹣2b,第三条边比第二条边短3a.
(1)则第二边的边长为 ,第三边的边长为 ;
(2)用含a,b的式子表示这个三角形的周长,并化简;
(3)若a,b满足|a﹣5|+(b﹣3)2=0,求出这个三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图A在数轴上所对应的数为﹣2.
(1)点B在点A右边距A点4个单位长度,求点B所对应的数;
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点 B 以每秒2个单位长度沿数轴向右运动,当点A运动到﹣6所在的点处时,求A,B两点间距离.
(3)在(2)的条件下,现A点静止不动,B点再以每秒2个单位长度沿数轴向左运动时,经过多长时间A,B两点相距4个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
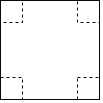
【题目】如图,把一边长为x厘米的正方形纸板的四个角各剪去一个边长为y厘米的小正方形,然后把它折成一个无盖纸盒.
(1)该纸盒的高是_____厘米,底面积是_____________平方厘米;
(2)求该纸盒的全面积(外表面积);
(3)为了使纸盒底面更加牢固且达到废物利用的目的,现考虑将剪下的四个小正方形平铺在盒子的底面,要求既不重叠又恰好铺满(不考虑纸板的厚度),求此时x与y之间的倍数关系.(直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
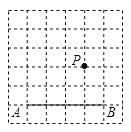
【题目】(2016浙江省温州市第20题)如图,在方格纸中,点A,B,P都在格点上.请按要求画出以AB为边的格点四边形,使P在四边形内部(不包括边界上),且P到四边形的两个顶点的距离相等.
(1)在图甲中画出一个ABCD.
(2)在图乙中画出一个四边形ABCD,使∠D=90°,且∠A≠90°.(注:图甲、乙在答题纸上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016山东省泰安市第17题)如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )
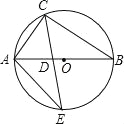
A.1:![]() B.1:
B.1:![]() C.1:2 D.2:3
C.1:2 D.2:3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com