
(满分12分)在平面直角坐标系中,抛物线 与
与 轴的两个交点
轴的两个交点
分别为A(-3,0)、B(1,0),过顶点C作CH⊥x轴于点H.
(1)直接填写: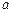 = ,b= ,顶点C的坐标为 ;
= ,b= ,顶点C的坐标为 ;
(2)在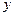 轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)若点P为x轴上方的抛物线上一动点(点P与顶点C不重合),PQ⊥AC于点Q,当△PCQ与△ACH相似时,求点P的坐标. 
解:(1)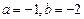 ,顶点C的坐标为(-1,4)………………………… 3分
,顶点C的坐标为(-1,4)………………………… 3分
(2)假设在y轴上存在满足条件的点D, 过点C作CE⊥y轴于点E.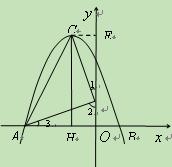
 由∠CDA=90°得,∠1+∠2="90°. " 又∠2+∠3=90°,
由∠CDA=90°得,∠1+∠2="90°. " 又∠2+∠3=90°,
∴∠3=∠1. 又∵∠CED=∠DOA =90°, ∴△CED∽△DOA,∴
∴△CED∽△DOA,∴ .
.



 设D(0,c),则
设D(0,c),则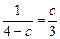 .
.
变形得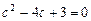 ,解之得
,解之得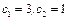 .
.
综合上述:在y轴上存在点D(0,3)或(0,1),
使△ACD是以AC为斜边的直角三角形. ………………………………… 7分
(3)①若点P在对称轴右侧(如图①),只能是△PCQ∽△CAH,得∠QCP=∠CAH.
延长CP交x轴于M,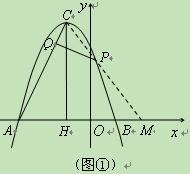
∴AM=CM, ∴AM2=CM2.
设M(m,0),则( m+3)2=42+(m+1)2,∴m=2,即M(2,0).
设直线CM的解析式为y=k1x+b1,
则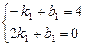 , 解之得
, 解之得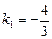 ,
,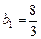 .
.
∴直线CM的解析式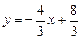 .…………………………………………… 8分
.…………………………………………… 8分
联立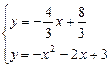 ,解之得
,解之得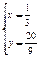 或
或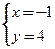 (舍去).∴
(舍去).∴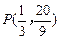 .…… 9分
.…… 9分
②若点P在对称轴左侧(如图②),只能是△PCQ∽△ACH,得∠PCQ=∠ACH.
过A作CA的垂线交PC于点F,作FN⊥x轴于点N.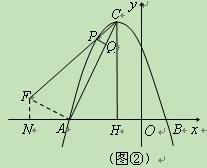
由△CFA∽△CAH得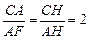 ,
,
由△FNA∽△AHC得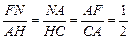 .
.
∴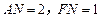 , 点F坐标为(-5,1). …………………………………10分
, 点F坐标为(-5,1). …………………………………10分
设直线CF的解析式为y=k2x+b2,则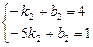 ,解之得
,解之得 .
.
∴直线CF的解析式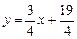 . ……………………………………………11分
. ……………………………………………11分
联立 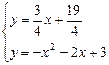 ,解之得
,解之得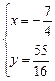 或
或 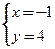 (舍去). ∴
(舍去). ∴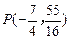 .
.
∴满足条件的点P坐标为 或
或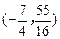 ………………………………12分
………………………………12分
解析


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
(本题满分12分)在平面直角坐标系![]() 中,已知二次函数
中,已知二次函数![]() 的图象与x轴交于A,B两点(点A在点B的左边),AB=4,与y轴交于点C,且过点(2,3).
的图象与x轴交于A,B两点(点A在点B的左边),AB=4,与y轴交于点C,且过点(2,3).
(1)求此二次函数的表达式;
(2)若抛物线的顶点为D,连接CD、CB,问抛物线上是否存在点P,使得∠PBC+∠BDC=90°. 若存在,求出点P的坐标;若不存在,请说明理由;
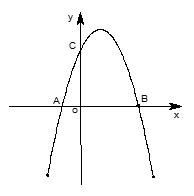 (3)点K抛物线上C关于对称轴的对称点,点G抛物线上的动点,在x轴上是否存在点F,使A、K、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由
(3)点K抛物线上C关于对称轴的对称点,点G抛物线上的动点,在x轴上是否存在点F,使A、K、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
(本题满分12分)在平面直角坐标系xOy中,边长为a(a为大于0的常数)的正方形ABCD的对角线AC、BD相交于点P,顶点A在x轴正半轴上运动,顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O),顶点C、D都在第一象限。
(1)当∠BAO=45°时,求点P的坐标;
(2)求证:无论点A在x轴正半轴上、点B在y轴正半轴上怎样运动,点P都在∠AOB的平分线上;
 (3)设点P到x轴的距离为h,试确定h的取值范围,并说明理由。
(3)设点P到x轴的距离为h,试确定h的取值范围,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
 轴于
轴于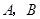 两点,交
两点,交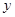 轴于点
轴于点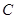 ,已知抛物线的对称轴为
,已知抛物线的对称轴为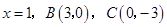 .
. |
 ,使点
,使点 到A、C两点间的距离之和最大.若存在,求出点
到A、C两点间的距离之和最大.若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. 轴上方平行于
轴上方平行于 轴的一条直线交抛物线于
轴的一条直线交抛物线于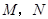 两点,以
两点,以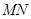 为直径作圆恰好与
为直径作圆恰好与 轴相切,求此圆的直径.
轴相切,求此圆的直径.查看答案和解析>>
科目:初中数学 来源:2011届山东省莱州一中初中毕业入学摸底考试数学试卷 题型:解答题
(本小题满分12分)在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.(1)求函数y= x+3的坐标三角形的三条边长; (2)若
x+3的坐标三角形的三条边长; (2)若
函数y= x+b(b为常数)的坐标三角形周长为16, 求此三角形面积.
x+b(b为常数)的坐标三角形周长为16, 求此三角形面积.
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市高新区2010-2011学年七年级下学期期末考试数学试题 题型:解答题
(本题满分12分)在平面直角坐标系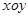 中,已知二次函数
中,已知二次函数 的图象与x轴交于A,B两点(点A在点B的左边),AB=4,与y轴交于点C,且过点(2,3).
的图象与x轴交于A,B两点(点A在点B的左边),AB=4,与y轴交于点C,且过点(2,3).
(1)求此二次函数的表达式;
(2)若抛物线的顶点为D,连接CD、CB,问抛物线上是否存在点P,使得∠PBC+∠BDC=90°. 若存在,求出点P的坐标;若不存在,请说明理由; (3)点K抛物线上C关于对称轴的对称点,点G抛物线上的动点,在x轴上是否存在点F,使A、K、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由
(3)点K抛物线上C关于对称轴的对称点,点G抛物线上的动点,在x轴上是否存在点F,使A、K、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com