练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    当a、b为何值时，多项式a2+2ab+2b2+6b+18有最小值？并求出这个最小值．

    解：a2+2ab+2b2+6b+18=a2+2ab+b2+b2+6b+9+9=（a+b）2+（b+3）2+9，
    ∴多项式的最小值为9．
    分析：把所给多项式整理为两个完全平方式相加的形式，括号外的常数即为多项式的最小值．
    点评：本题考查了配方法的应用及非负数的性质，解决本题的关键是把所给多项式整理为两个完全平方式相加的形式；难点是根据得到的式子判断出所求的最小值．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    甲、乙两人同时从宁波港出发到距离240千米的上海港，甲乘快艇4小时候到达上海港，然后立即换成船返回宁波港，乙乘船经12小时到达上海港，此时甲也正好返回到宁波港，如图表示甲、乙在行进过程中离宁波港的距离y（千米）与出发时间x（时）之间的函数关系．（船、快艇的长度忽略不计）
    （1）当x=4时，甲、乙相距多远？
    （2）当出发时间x为何值时，甲、乙离宁波港的距离相等？
    （3）若海面上相距不超过120千米时，能相互接收对讲信号，求甲乙可以相互接收对讲信号时x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源：新课标　1＋1轻巧夺冠·优化训练　(人教版)七年级数学(下) 人教版　新课标　银版 题型：044

    已知方程组

    ①当a，b为何值时，此方程组无解．

    ②当a，b为何值时，此方程组有唯一解．

    ③当a，b为何值时，此方程组有无穷多组解．

    查看答案和解析>>

    科目：初中数学 来源：新教材新学案　数学　七年级下册 题型：044

    当m，n为何值时，方程组

    (1)有唯一解；

    (2)有无数多个解；

    (3)无解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

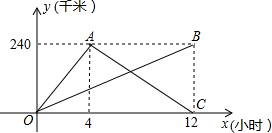    甲、乙两人同时从宁波港出发到距离240千米的上海港，甲乘快艇4小时候到达上海港，然后立即换成船返回宁波港，乙乘船经12小时到达上海港，此时甲也正好返回到宁波港，如图表示甲、乙在行进过程中离宁波港的距离y（千米）与出发时间x（时）之间的函数关系．（船、快艇的长度忽略不计）
    （1）当x=4时，甲、乙相距多远？
    （2）当出发时间x为何值时，甲、乙离宁波港的距离相等？
    （3）若海面上相距不超过120千米时，能相互接收对讲信号，求甲乙可以相互接收对讲信号时x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源：同步题 题型：解答题

    已知方程  
    （1）当a、b为何值时，此方程组无解；  
    （2）当a、b为何值时，此方程组有唯一解；  
    （3）当a、b为何值时，此方程组有无穷多组解。

    查看答案和解析>>

    同步练习册答案