
 已知:反比例函数
已知:反比例函数 和
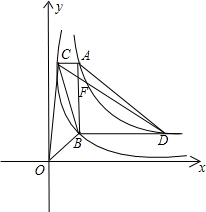
和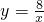 在平面直角坐标系xOy第一象限中的图象如图所示,点A在
在平面直角坐标系xOy第一象限中的图象如图所示,点A在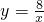 的图象上,AB∥y轴,与
的图象上,AB∥y轴,与 的图象交于点B,AC、BD与x轴平行,分别与
的图象交于点B,AC、BD与x轴平行,分别与 、
、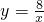 的图象交于点C、D.
的图象交于点C、D. 的值.
的值. 得y=4,则A点坐标为(2,4),
得y=4,则A点坐标为(2,4),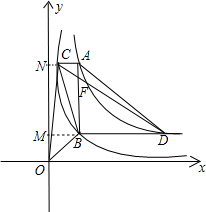
 得x=
得x= ;把x=2代入y=
;把x=2代入y= 得y=1,
得y=1, ,4),B点坐标为(2,1),
,4),B点坐标为(2,1), 得x=8,
得x=8, ,4)、D(8,1)代入
,4)、D(8,1)代入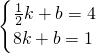 ,解得
,解得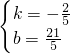 ,
, x+
x+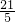 ;
; ),C点坐标为(
),C点坐标为( ,
, ),B点坐标为(m,
),B点坐标为(m, ),D点坐标为(4m,
),D点坐标为(4m, ),
), =
= ,BD=4m-m=3m,AB=
,BD=4m-m=3m,AB= -
- =
= ,
, (
( +3m)•
+3m)• =
= ;
; ×2=1,S梯形BMNC=
×2=1,S梯形BMNC= (
( +m)•
+m)• =
= ,
, ,
,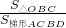 =
=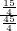 =
= .
. 的图象上可确定A点坐标为(2,4),则根据AC∥x轴,AB∥y轴得到C点的纵坐标为4,B点的横坐标为2,再利用C、B在y=
的图象上可确定A点坐标为(2,4),则根据AC∥x轴,AB∥y轴得到C点的纵坐标为4,B点的横坐标为2,再利用C、B在y= 的图象上可确定C点坐标为(
的图象上可确定C点坐标为( ,4),B点坐标为(2,1);由于BD∥x轴,则D点的纵坐标与B的纵坐标相等,根据D点在y=
,4),B点坐标为(2,1);由于BD∥x轴,则D点的纵坐标与B的纵坐标相等,根据D点在y= 的图象上可确定D点坐标为(8,1),然后利用待定系数法求出直线CD的解析式;
的图象上可确定D点坐标为(8,1),然后利用待定系数法求出直线CD的解析式; ),C点坐标为(
),C点坐标为( ,
, ),B点坐标为(m,
),B点坐标为(m, ),D点坐标为(4m,
),D点坐标为(4m, ),根据比例系数的几何意义得到S△OCN=S△OBM=1,根据梯形的面积公式得到S梯形BMNC=
),根据比例系数的几何意义得到S△OCN=S△OBM=1,根据梯形的面积公式得到S梯形BMNC= ,S梯形ACBD=
,S梯形ACBD= ;再利用S四边形BONC=S△ONC+S△OBC=S梯形BMNC+S△OBM得S△OBC=S梯形BMNC=
;再利用S四边形BONC=S△ONC+S△OBC=S梯形BMNC+S△OBM得S△OBC=S梯形BMNC= ,最后计算
,最后计算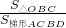 的值.
的值.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:第20章《二次函数和反比例函数》常考题集(44):20.7 反比例函数的图象、性质和应用(解析版) 题型:解答题
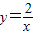 和
和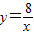 在平面直角坐标系xOy第一象限中的图象如图所示,点A在
在平面直角坐标系xOy第一象限中的图象如图所示,点A在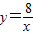 的图象上,AB∥y轴,与
的图象上,AB∥y轴,与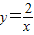 的图象交于点B,AC、BD与x轴平行,分别与
的图象交于点B,AC、BD与x轴平行,分别与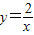 ,
,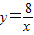 的图象交于点C、D.
的图象交于点C、D.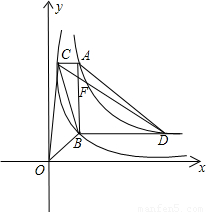
查看答案和解析>>
科目:初中数学 来源:2012年北京市中考数学二模练习试卷(二)(解析版) 题型:解答题
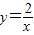 和
和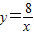 在平面直角坐标系xOy第一象限中的图象如图所示,点A在
在平面直角坐标系xOy第一象限中的图象如图所示,点A在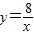 的图象上,AB∥y轴,与
的图象上,AB∥y轴,与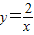 的图象交于点B,AC、BD与x轴平行,分别与
的图象交于点B,AC、BD与x轴平行,分别与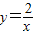 ,
,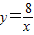 的图象交于点C、D.
的图象交于点C、D.
查看答案和解析>>
科目:初中数学 来源:2012年浙江省杭州市文澜中学中考数学模拟试卷(解析版) 题型:解答题
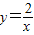 和
和 在平面直角坐标系xOy第一象限中的图象如图所示,点A在
在平面直角坐标系xOy第一象限中的图象如图所示,点A在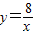 的图象上,AB∥y轴,与
的图象上,AB∥y轴,与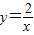 的图象交于点B,AC、BD与x轴平行,分别与
的图象交于点B,AC、BD与x轴平行,分别与 ,
,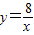 的图象交于点C、D.
的图象交于点C、D.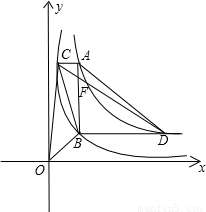
查看答案和解析>>
科目:初中数学 来源:2010年吉林省珲春市珲春四中中考数学模拟试卷(解析版) 题型:解答题
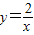 和
和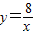 在平面直角坐标系xOy第一象限中的图象如图所示,点A在
在平面直角坐标系xOy第一象限中的图象如图所示,点A在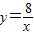 的图象上,AB∥y轴,与
的图象上,AB∥y轴,与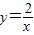 的图象交于点B,AC、BD与x轴平行,分别与
的图象交于点B,AC、BD与x轴平行,分别与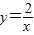 ,
, 的图象交于点C、D.
的图象交于点C、D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com