练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5、随着多边形边数的增加，每增加一条边，则（　　）
    分析：利用多边形的内角和定理和外角和特征即可解决问题．
    解答：解：∵n边形的内角和是（n-2）•180°，
    当边数增加一条就变成n+1，则内角和是（n-1）•180度，
    内角和增加：（n-1）•180°-（n-2）•180°=180°；
    根据多边形的外角和特征，边数变化外角和不变．
    故选C．
    点评：本题主要考查了多边形的内角和定理与外角和特征．先设这是一个n边形是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

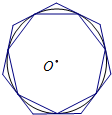    （2013•北仑区二模）割圆术是我国古代数学家刘徽创造的一种求周长和面积的方法：随着圆内接正多边形边数的增加，它的周长和面积越来越接近圆周长和圆面积，“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”．试用这个方法解决问题：如图，⊙的内接多边形周长为3，⊙O的外切多边形周长为3.4，则下列各数中与此圆的周长最接近的是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    随着多边形边数的增加，每增加一条边，则


    1. A.
      外角和增加180°
    2. B.
      对角线增加1条
    3. C.
      内角和增加180°
    4. D.
      内角和增加360°

    查看答案和解析>>

    科目：初中数学 来源：江苏省期末题 题型：单选题

    随着多边形边数的增加，每增加一条边，则
    [     ]
    A．外角和增加180°
    B．对角线增加1条
    C．内角和增加180°
    D．内角和增加360°

    查看答案和解析>>

    科目：初中数学 来源：江苏期末题 题型：单选题

    随着多边形边数的增加，每增加一条边，则
    [     ]
    A．外角和增加180°
    B．对角线增加1条
    C．内角和增加180°
    D．内角和增加360°

    查看答案和解析>>

    同步练习册答案