如图，只要( )，则△ABC≌△ADC
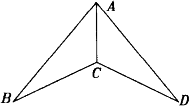
A．AB＝AD，∠B＝∠D
B．AB＝AD，∠ACB＝∠ACD
C．BC＝DC，∠BAC＝∠DAC
D．AB＝AD，∠DAC＝∠BAC
科目：初中数学 来源：数学教研室 题型：022
要将图乙中的马走到指定的位置P处，即从（四，6）走到(六，4)，现提供一种走法：
(四，6)→(六，5)→(四，4)→(五，2)→(六，4)
甲 乙
(1)下面是提供的另一走法，请你填上其中所缺的一步：
(四，6)→(五，8)→(七，7)→________→(六，4)
(2)请你再给出另一种走法(只要与前面的两种走法不完全相同即可，步数不限)，你的走法是：
查看答案和解析>>
科目：初中数学 来源：数学教研室 题型：044
三角形内角平分线性质定理：三角形的内角平分线分对边所得的线段与两
边对应成比例。
已知：如图，在△ABC中，AD是角平分线。
求证：
＝
。
分析：要证
＝
，一般只要证BD、DC与AB、AC
或BD、AB与DC、AC所在的三角形相似即可，现在点B、D、C
在一条直线上，△ABD与△ADC不相似，需要考虑用别的方法换比。在比例式
＝
中，AC恰是BD、DC、AB的第四比例项，所以考虑过点C作CE//AD，交
BA的延长线于点E，从而得到BD、DC、AB的第四比例项AE，这样，证明
＝
就可以转化成证AE＝AC。
证明：过点C作CE//DA交BA的延长线于点E。
。
（1）在上述证明过程中，用到了哪些定理？（写对两个定理即可）
（2）在上述分析、证明过程中，主要利用到了下列三种数学思想中的哪一种？选出一
个填在后面的括号内………………………………………………………………（ ）
A. 数形结合思想 B. 转化思想 C. 分类讨论思想
（3）用三角形内角平分线性质定理解答问题。
如下图，已知在△ABC中，AD是角平分线，AB＝5cm，AC＝4cm，
BC＝7cm，求BD的长。
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
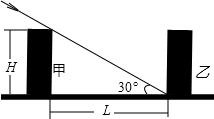下表所示．仅就图中居民楼乙的采光问题，你认为哪种方案设计较为合理，并说明理由．（参考数据
=1.732）| A | B | C | D | |
| H（米） | 12 | 15 | 16 | 18 |
| L（米） | 18 | 25 | 28 | 30 |
查看答案和解析>>
科目：初中数学 来源： 题型：
在直角梯形ABCD中，AD∥BC，∠B=∠A=90°.
操作示例
小明取直角梯形ABCD的非直角腰CD的中点P，过点P作PE∥AB，剪下△PEC（如图1），并将△PEC绕点P按逆时针方向旋转180°到△PFD的位置，拼成新的图形（如图2）．
（Ⅰ）思考与实践：
（1）操作后小明发现，拼成的新图形是矩形，请帮他说明理由；
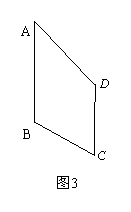
（2）类比图2的剪拼方法，请你在图3画出剪拼成一个平行四边形的示意图．
 |
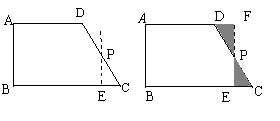图1 图2
（Ⅱ）发现与运用：
小白发现：在一个四边形中，只要有一组对边平行，就可以剪拼成平行四边形．
请你选择下面两题中的一题作答：（多做不加分，两题都做按第一题计分）
图4
(1)如图4，在梯形ABCD中，AD∥BC，E是CD的中点， EF⊥AB于点F，AB=5，EF=4，求梯形ABCD的面积。
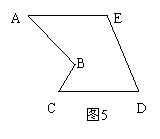
（2）如图5的多边形中，AE=CD，AE∥CD，能否沿一条直线进行剪切，拼成一个平行四边形？若能，请你在图中画出剪拼的示意图并作必要的文字说明；若不能，简要说明理由．
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
