Question

下列结论不正确的是

1. A.
   
   如图，若PA=PB，∠APB=2∠ACB，AC与PB交于点D，且PB=4，PD=3，则AD•DC等于6
2. B.
   
   M是△ABC的内心，∠BMC=130°，则∠A的度数为50°
3. C.
   
   如图，⊙O中，弦AD∥BC，DA=DC，∠AOC=160°，则∠BCO等于80°
4. D.
   若一圆锥的轴截面是等边三角形，则其侧面展开图的圆心角是120°

Answer 1

A
分析：以P为圆心，以PA=PB为半径作圆，延长BD交圆于M，根据相交弦定理求出即可；求出∠ABC+∠ACB的度数，根据三角形的内角和定理求出即可；求出∠ADC，根据等腰三角形性质求出∠DCO，根据平行线性质求出即可；根据弧长公式求出即可．
解答：A、以P为圆心，以PA=PB为半径作圆，延长BD交圆于M，

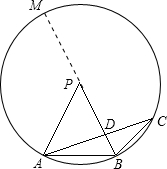
则有：PA=PB=4，∠APB=2∠ACB，AC与PB交于点D，PD=3，
设∠ACB=θ，则∠APM=2θ，又∠ACB=θ，∴C在圆上．
∴AD•DC=BD•DM=BD•（PM+PD）=1•（4+3）=7，故本选项错误；
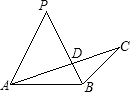
B、∵M是△ABC的内心，∠BMC=130°，
∴∠MBC+∠MCB=180°-130°=50°，
∴∠ABC+∠ACB=2×50°=100°，
∴∠A=180°-100°=80°，故本选项错误；
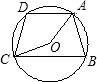
C、连接AC，

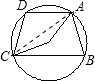
∵∠B=∠AOC=80°，
∴∠ADC=180°-80°=100°，
∵AD=DC，
∴∠DCA=∠DAC=（180°-100°）=40°，
同理∠AC0=10°，
∵AD∥BC，
∴∠ADC+∠DCB=180°，∴∠BCO=30°，故本选项错误；
D、设半径是a，则等边三角形的边长是2a，
∴2πa=，
解得：n=180，故本选项错误；
故答案都不对．
点评：本题主要考查对三角形的内角和定理，相交弦定理，等腰三角形的性质，圆内接四边形的性质，三角形的内切圆等知识点的理解和掌握，综合运用性质进行推理是解此题的关键．