
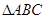 内接于⊙O,
内接于⊙O, 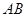 为⊙O的直径,
为⊙O的直径,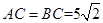 , 点
, 点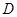 是
是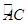 上一个动点,连结
上一个动点,连结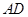 、
、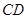 和
和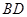 ,
, 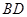 与
与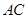 相交于点
相交于点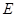 , 过点
, 过点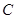 作
作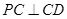 于
于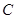 ,
, 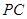 与
与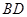 相交于点
相交于点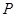 ,连结
,连结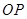 和
和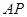 .
.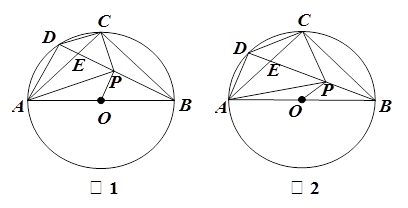
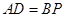 ;
;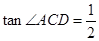 , 求证:
, 求证: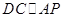 ;
;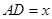 , 四边形
, 四边形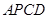 的面积为
的面积为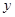 ,求
,求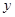 与
与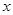 之间的关系式.
之间的关系式.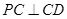 ,
, 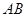 为
为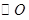 的直径
的直径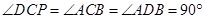
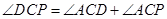 ,
,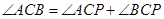
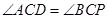

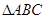 是等腰直角三角形
是等腰直角三角形 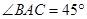
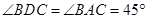
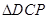 是等腰直角三角形
是等腰直角三角形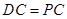
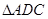 ≌
≌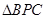
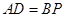
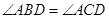
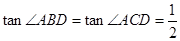
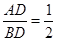
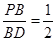
 是
是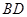 的中点
的中点 
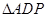 是等腰直角三角形
是等腰直角三角形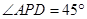
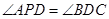
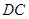 ∥
∥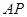
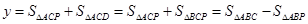
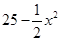 (
(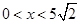 )
) 和x,利用三角形的面积公式即可表示出y与x的函数关系式,同时求出自变量x的范围.
和x,利用三角形的面积公式即可表示出y与x的函数关系式,同时求出自变量x的范围.

 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源:不详 题型:单选题
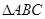 内接于⊙
内接于⊙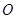 ,
,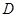 为线段
为线段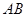 的中点,延长
的中点,延长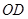 交⊙
交⊙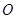 于点
于点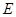 ,连结
,连结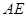 ,
,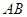 ,则下列五个结论:①
,则下列五个结论:①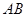 ⊥
⊥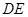 ,②
,②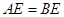 ,③
,③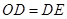 ,④
,④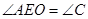 ,⑤
,⑤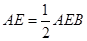 ,正确结论的个数有( )
,正确结论的个数有( )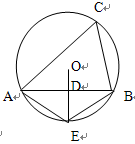
A.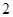 个 个 | B.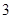 个 个 | C.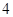 个 个 | D.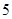 个 个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com