
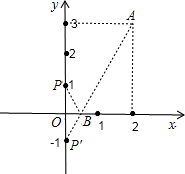
 解:(1)P(0,1)向上平移3个单位后的坐标是(0,1+3),即(0,4);
解:(1)P(0,1)向上平移3个单位后的坐标是(0,1+3),即(0,4);
|
|
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
| π |
| 3 |
 |
| ADF |
查看答案和解析>>
科目:初中数学 来源: 题型:
 20、岳飞是我国古代宋朝的民族英雄,曾任通泰镇抚史、兼泰州知州、据说在泰州抗击金兵期间,有一次曾向将领们讲了如下一个布阵图,如图4是一座城池,在城池的四周设了八个哨所,一共由24个卫士把守,按直线算,每边都有11个人,后来由于军情发生变化,连续四次给哨所增添兵力,每次增加4人,但要求在增加人员后,仍然保持每边11个人把守、请问,兵力应如何调整?
20、岳飞是我国古代宋朝的民族英雄,曾任通泰镇抚史、兼泰州知州、据说在泰州抗击金兵期间,有一次曾向将领们讲了如下一个布阵图,如图4是一座城池,在城池的四周设了八个哨所,一共由24个卫士把守,按直线算,每边都有11个人,后来由于军情发生变化,连续四次给哨所增添兵力,每次增加4人,但要求在增加人员后,仍然保持每边11个人把守、请问,兵力应如何调整?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
 留一位小数)
留一位小数)查看答案和解析>>
科目:初中数学 来源: 题型:
 9、如图,8×8方格纸上的两条对称轴EF,MN相交于中心点O,对△ABC分别作下列变换:
9、如图,8×8方格纸上的两条对称轴EF,MN相交于中心点O,对△ABC分别作下列变换:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com