
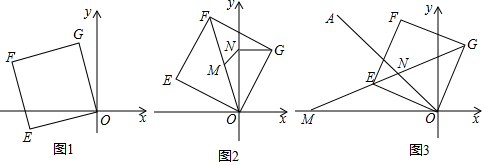
分析 (1)如图1中,连接OF、EG,OF交EG于K,作GM⊥y轴于M,EN⊥y轴于N.由△EON≌△GOM,推出GM=ON=1,EN=OM=3,推出E(-3,-1),求出点K的坐标即可解决问题;
(2)结论:∠MNO=45°,不发生变化.如图2中,作MH⊥y轴于H,MJ⊥GN于J,连接GM.只要证明△OMH≌△JMG,推出MJ=MH,又MH⊥y轴于H,MJ⊥GN于J,即可推出MN平分∠HNJ,由此即可解决问题;
(3)结论:①MN2=ME2+NG2正确.如图3中,将△MOE绕点O顺时针性质90°得到△OKG.首先证明△NGK是直角三角形,再证明△NOM≌△NOK即可解决问题;
解答 解:(1)如图1中,连接OF、EG,OF交EG于K,作GM⊥y轴于M,EN⊥y轴于N.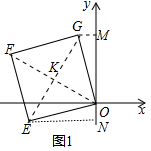
∵四边形OEFG是正方形,
∴OG=OE,∠EOG=∠GMO=∠ENO=90°,FK=OK,KG=KE,
∴∠EON+∠GOM=90°,∠GOM+∠OGM=90°,
∴∠EON=∠OGM,
∴△EON≌△GOM,
∴GM=ON=1,EN=OM=3,
∴E(-3,-1),
∴K(-2,1),
∴F(-4,2).
(2)结论:∠MNO=45°,不发生变化.
理由:如图2中,作MH⊥y轴于H,MJ⊥GN于J,连接GM.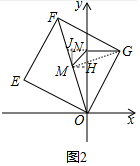
∵MF=MO,∠FGO=90°,FG=GO,
∴GM=OM=FM,GM⊥OF,
∵∠MJN=∠MHN=∠JNH=90°,
∴∠HMJ=∠OMG=90°,
∴∠JMG=∠OMH,
∵∠MHO=∠MJG=90°,
∴△OMH≌△JMG,
∴MJ=MH,∵MH⊥y轴于H,MJ⊥GN于J,
∴MN平分∠HNJ,
∴∠MNO=45°.
(3)结论:①MN2=ME2+NG2正确.
理由:如图3中,将△MOE绕点O顺时针性质90°得到△OKG.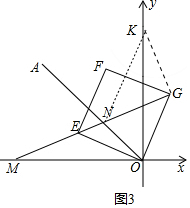
∵∠OEM=∠OGK=135°,
∵∠EGO=45°,
∴∠NGK=90°,
∵A(-6,6),
∴∠NOM=∠NOK,
∵ON=ON,OM=OK,
∴△NOM≌△NOK,
∴MN=KN,
在Rt△KNG中,∵NK2=GN2+KG2,KG=EM,
∴MN2=NG2+EM2.
点评 本题考查四边形综合题、正方形的性质、全等三角形的判定和性质、中点坐标公式、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
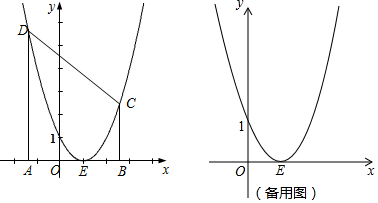
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
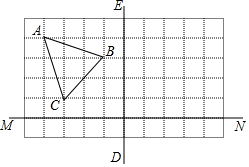 如图,在所给正方形网格图中完成下列各题:
如图,在所给正方形网格图中完成下列各题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠ACB=90°,BC=AC=4,M为AB中点,D是射线BC上的一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ED、ME,点D在运动过程中ME的最小值为2.
如图,在△ABC中,∠ACB=90°,BC=AC=4,M为AB中点,D是射线BC上的一动点,连接AD,将线段AD绕点A逆时针旋转90°得到线段AE,连接ED、ME,点D在运动过程中ME的最小值为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
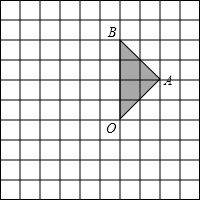 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点,△ABO的三个顶点A、B、O都在格点上.
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点,△ABO的三个顶点A、B、O都在格点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com