练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．先化简再求值：$\frac{x+3}{x-2}÷（{x+2-\frac{5}{x-2}}）$，其中x是不等式组$\left\{\begin{array}{l}x-3（x-3）≥1\\ 4x-2＜5x-3\end{array}$的一个整数解．

    分析 原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，求出不等式组的整数解得到x的值，代入计算即可求出值．

    解答 解：原式=$\frac{x+3}{x-2}$•$\frac{x-2}{（x+3）（x-3）}$
    =$\frac{1}{x-3}$，
    解不等式组得1＜x≤4，
    符合不等式解集的整数是2，3，4，
    当x=4时，原式=1．

    点评 此题考查了分式的化简求值，以及一元一次不等式组的整数解，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    5．（1）计算：（-$\frac{1}{3}$）-1-$\sqrt{18}$+（$\sqrt{3}$-$\sqrt{2}$）0+6sin45°
    （2）化简：1-$\frac{x-2}{x+1}$÷$\frac{{x}^{2}-4}{{x}^{2}+2x+1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．已知关于x的一元二次方程x2-2x+k-1=0．
    （1）若此方程有两个不相等的实数根，求实数k的取值范围；
    （2）已知x=3是此方程的一个根，求方程的另一个根及k的值；
    （3）当Rt△ABC的斜边长c=$\sqrt{3}$，且两条直角边a和b恰好是这个方程的两个根时，求Rt△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

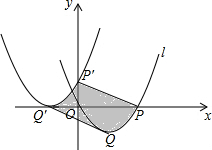    3．如图，抛物线l：y=2x2-2x，将该抛物线向左并向上平移，使顶点Q的对应点是Q′，抛物线l与x轴的右交点P的对应点是P′，点P′、Q′都在坐标轴上，则在这个平移的过程中，抛物线l上曲线段PQ扫过的面积（即图中阴影部分的面积）为$\frac{3}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．若a-b=3，ab=2，则a2b-ab2=6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．函数y=-mx2+m与y=$\frac{m}{x}$（x≠0）在同一坐标系中的图象大致可能是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

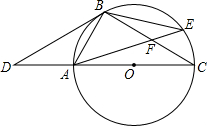    7．如图，点D是⊙O的直径CA延长线上的一点，点B在⊙O上，且AB=AD=AO．
    （1）求证：BD是⊙O的切线；
    （2）若点E是劣弧BC上一点，AE与BC相交于点F，且∠ABE=105°，S△BEF=8（$\sqrt{3}$-1），求△ACF的面积和CF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．若不等式组$\left\{\begin{array}{l}{\frac{1}{2}x-1＜0}\\{-x＜-m}\end{array}\right.$有解，则m的取值范围在数轴上表示为（　　）
    A．B．
    C．D．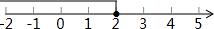

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

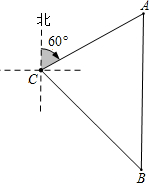    5．在甲、乙两地之间需修一南北走向的隧道AB．从入口B的西北方向600米的C点处，测得另一入口A在C点的北偏东60°的方向上，求隧道AB的长（最后结果保留整数）．（参考数据：$\sqrt{2}≈1.414\;，\sqrt{3}≈1.732，\sqrt{6}$≈2.449）．

    查看答案和解析>>

    同步练习册答案