
如图,AP为⊙O的直径,B、C为⊙O上的点,BC∥OA且BC=OA,则∠P= 度。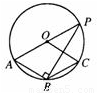
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:阅读理解
 面问题:若y=
面问题:若y=| x2+1 |
| (9-x)2+4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
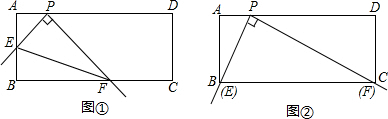
 尺放在给出的图形上,使直角顶点P在线段EF(包括端点)上滑动,直角的一边始终经过点C,另一边与BF相交于G,连接AP.
尺放在给出的图形上,使直角顶点P在线段EF(包括端点)上滑动,直角的一边始终经过点C,另一边与BF相交于G,连接AP.| 1 |
| 2 |
| 9 |
| 8 |
| 7 |
| 4 |
| 10 |
| 7 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 5 |
| 5 |
| PF |
| PE |
查看答案和解析>>
科目:初中数学 来源:2012届浙江省嵊州市初中毕业生学业评价调测数学试卷(带解析) 题型:解答题
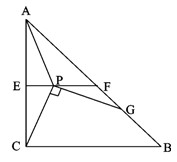
如图,Rt△ABC中,∠C= Rt∠,AC=BC=2,E,F分别为AC,AB的中点,连结EF。
现将一把直角尺放在给出的图形上,使直角顶点P在线段EF(包括端点)上滑动,直角的
一边始终经过点C,另一边与BF相交于G,连结AP。
(1)求证:PC=PA=PG;
(2)设EP=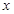 ,四边形BCPG的面积为
,四边形BCPG的面积为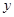 ,求
,求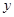 与
与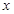 之间的函数解析式,现有三个数
之间的函数解析式,现有三个数 ,
, ,
, 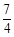 试通过计算说明哪几个数符合
试通过计算说明哪几个数符合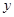 值的要求,并求出符合
值的要求,并求出符合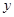 值时的
值时的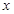 的值。
的值。
(3)当直角顶点P滑动到点F时,再将直角尺绕点F顺时针旋转,两直角边分别交AC,BC于点M,N,连结MN。当旋转到使 时,求△APM的周长。
时,求△APM的周长。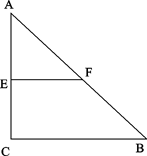

查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省嵊州市初中毕业生学业评价调测数学试卷(解析版) 题型:解答题
如图,Rt△ABC中,∠C= Rt∠,AC=BC=2,E,F分别为AC,AB的中点,连结EF。
现将一把直角尺放在给出的图形上,使直角顶点P在线段EF(包括端点)上滑动,直角的
一边始终经过点C,另一边与BF相交于G,连结AP。
(1)求证:PC=PA=PG;
(2)设EP=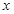 ,四边形BCPG的面积为
,四边形BCPG的面积为 ,求
,求 与
与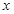 之间的函数解析式,现有三个数
之间的函数解析式,现有三个数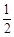 ,
, ,
,
 试通过计算说明哪几个数符合
试通过计算说明哪几个数符合 值的要求,并求出符合
值的要求,并求出符合 值时的
值时的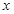 的值。
的值。
(3)当直角顶点P滑动到点F时,再将直角尺绕点F顺时针旋转,两直角边分别交AC,BC于点M,N,连结MN。当旋转到使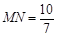 时,求△APM的周长。
时,求△APM的周长。


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com