
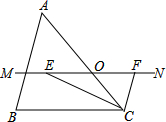
 如图,△ABC中,点O是AC上一动点,过点O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACH的平分线于点F.
如图,△ABC中,点O是AC上一动点,过点O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACH的平分线于点F. (1)证明:∵MN∥BC,
(1)证明:∵MN∥BC,

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 一个纸盒里有红、黄、蓝、绿四种颜色的小球,这些小球除颜色不同外其余都完全相同,如图是各个颜色小球数量的统计图,如果小红从箱子中拿出一个小球,那么拿到绿色小球的可能性大小为
一个纸盒里有红、黄、蓝、绿四种颜色的小球,这些小球除颜色不同外其余都完全相同,如图是各个颜色小球数量的统计图,如果小红从箱子中拿出一个小球,那么拿到绿色小球的可能性大小为查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,一张直角三角形纸片,两直角边AC=6cm,BC=8cm,∠C=90°,现将三角形沿AD对折,直角边AC落在AB上,点C落在点E处,求折叠后部分△ADE的面积.
如图,一张直角三角形纸片,两直角边AC=6cm,BC=8cm,∠C=90°,现将三角形沿AD对折,直角边AC落在AB上,点C落在点E处,求折叠后部分△ADE的面积.查看答案和解析>>
科目:初中数学 来源: 题型:
| 每箱总质量 (kg) | 每箱中大五星与小五星的质量比 | 包装费 (元/箱) | 售价 (元/箱) | |
| A种搭配 | 12 | 2:1 | 4 | 105 |
| B种搭配 | 12 | 1:1 | 4 | 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com