Question

17．如图，在平面直角坐标系xOy中，三角板的直角顶点P的坐标为（2，2），一条直角边与x轴的正半轴交于点A，另一直角边与y轴交于点B，三角板绕点P在坐标平面内转动的过程中，当△POA为等腰三角形时，请写出所有满足条件的点B的坐标（0，2），（0，0），（0，4-2$\sqrt{2}$）．

Answer 1

分析 由P坐标为（2，2），可得∠AOP=45°，然后分别从OA=PA，OP=PA，OA=OP去分析求解即可求得答案．

解答 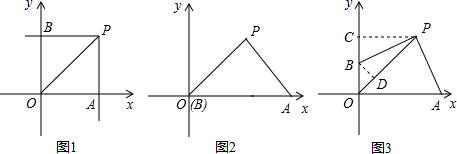解：∵P坐标为（2，2），
∴∠AOP=45°，
①如图1，若OA=PA，则∠AOP=∠OPA=45°，
∴∠OAP=90°，
即PA⊥x轴，
∵∠APB=90°，
∴PB⊥y轴，
∴点B的坐标为：（0，2）；
②如图2，若OP=PA，则∠AOP=∠OAP=45°，
∴∠OPA=90°，
∵∠BPA=90°，
∴点B与点O重合，
∴点B的坐标为（0，0）；
③如图3，若OA=OP，则∠OPA=∠OAP=$\frac{180°-∠AOP}{2}$=67.5°，
过点P作PC⊥y轴于点C，过点B作BD⊥OP于点D，
则PC∥OA，
∴∠OPC=∠AOP=45°，
∵∠APB=90°，
∴∠OPB=∠APB-∠OPA=22.5°，
∴∠OPB=∠CPB=22.5°，
∴BC=BD，
设OB=a，
则BD=BC=2-a，
∵∠BOP=45°，
在Rt△OBD中，BD=OB•sin45°，
即2-a=$\frac{\sqrt{2}}{2}$a，
解得：a=4-2$\sqrt{2}$．
综上可得：点B的坐标为：（0，2），（0，0），（0，4-2$\sqrt{2}$）．
故答案为：（0，2），（0，0），（0，4-2$\sqrt{2}$）．

点评 此题考查了等腰三角形的性质、三角函数的定义以及旋转的性质．此题难度较大，注意掌握方程思想、分类讨论思想以及数形结合思想的应用．