
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
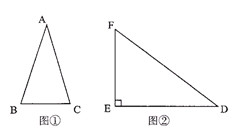
阅读理解:通过学习三角函数,我们知道在直角三角形中,一个锐角的大小,与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化。类似地,可以在等腰三角形中,建立边角之间的联系。我们定义:等腰三角形中底边长与腰长的比叫做顶角正对(sad)。如图1,在⊿ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=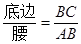 。容易知道一个角的大小,与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解下列问题:
。容易知道一个角的大小,与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解下列问题:
1.计算:sad60°= ▲
2.对于0°<A<90°,∠A的正对值sadA的取值范围是 ▲ ;
3.如图2,已知△DEF中,∠E=90°,cosD=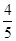 ,试求sadD的值。
,试求sadD的值。
查看答案和解析>>
科目:初中数学 来源:2014届北京第一六一中学七年级上学期期中测试数学试卷(解析版) 题型:填空题
定义计算“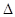 ”,对于两个有理数
”,对于两个有理数 ,
,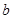 ,有
,有
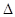
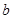 =
=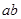 -(
-( +
+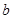 ),例如:
),例如:
-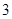
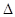
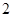 =
=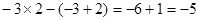 ,则
,则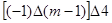 =___
__。
=___
__。
查看答案和解析>>
科目:初中数学 来源:2011-2012学年福建永安九年级学业质量检测考试数学试卷(解析版) 题型:解答题
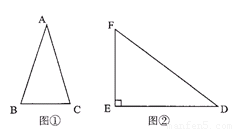
阅读理解:通过学习三角函数,我们知道在直角三角形中,一个锐角的大小,与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化。类似地,可以在等腰三角形中,建立边角之间的联系。我们定义:等腰三角形中底边长与腰长的比叫做顶角正对(sad)。如图1,在⊿ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=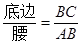 。容易知道一个角的大小,与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解下列问题:
。容易知道一个角的大小,与这个角的正对值也是相互唯一确定的。根据上述角的正对定义,解下列问题:
1.计算:sad60°= ▲
2.对于0°<A<90°,∠A的正对值sadA的取值范围是 ▲ ;
3.如图2,已知△DEF中,∠E=90°,cosD=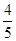 ,试求sadD的值。
,试求sadD的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com