

| A. | π | B. | $\sqrt{2}$π | C. | 1.6π | D. | $\frac{3}{2}$π |
分析 先找出计算直角三角形内切圆半径的规律:半径r=$\frac{a+b+c}{2}$,长特殊到一般,探究规律后,利用规律即可解决问题.
解答 解:图1,过点O做OE⊥AC,OF⊥BC,垂足为E、F,则∠OEC=∠OFC=90°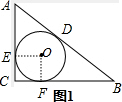
∵∠C=90°
∴四边形OECF为矩形
∵OE=OF
∴矩形OECF为正方形
设圆O的半径为r,则OE=OF=r,AD=AE=3-r,BD=4-r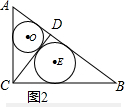
∴3-r+4-r=5,r=$\frac{3+4-5}{2}$=1
∴S1=π×12=π
图2,由S△ABC=$\frac{1}{2}$×3×4=$\frac{1}{2}$×5×CD
∴CD=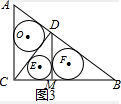 $\frac{12}{5}$由勾股定理得:AD=$\sqrt{{3}^{2}-(\frac{12}{5})^{2}}$=$\frac{9}{5}$,BD=5-$\frac{9}{5}$=$\frac{16}{5}$,
$\frac{12}{5}$由勾股定理得:AD=$\sqrt{{3}^{2}-(\frac{12}{5})^{2}}$=$\frac{9}{5}$,BD=5-$\frac{9}{5}$=$\frac{16}{5}$,
由(1)得:
⊙O的半径=$\frac{\frac{9}{5}+\frac{12}{5}-3}{2}$=$\frac{3}{5}$,⊙E的半径=$\frac{\frac{12}{5}+\frac{16}{5}-4}{2}$=$\frac{4}{5}$
∴S1+S2=π×( $\frac{3}{5}$)2+π×( $\frac{4}{5}$)2=π.
图3,由S△CDB=$\frac{1}{2}$×$\frac{12}{5}$×$\frac{16}{5}$=$\frac{1}{2}$×4×MD
∴MD=$\frac{48}{25}$
由勾股定理得:CM=$\sqrt{(\frac{12}{5})^{2}-(\frac{48}{25})^{2}}$=$\frac{36}{25}$,MB=4-$\frac{36}{25}$=$\frac{64}{25}$
由(1)得:⊙O的半径=$\frac{3}{5}$,:⊙E的半径=$\frac{\frac{48}{25}+\frac{36}{25}-\frac{12}{5}}{2}$=$\frac{12}{25}$
∴⊙F的半径=$\frac{\frac{48}{25}+\frac{64}{25}-\frac{16}{5}}{2}$=$\frac{16}{25}$
∴S1+S2+S3=π×( $\frac{3}{5}$)2+π×( $\frac{12}{25}$)2+π×( $\frac{16}{25}$)2=π
…
观察规律可知S1+S2+S3+…+S6=π.
故选A.
点评 本题考查了直角三角形的内切圆,这是一个图形变化类的规律题,首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解;解决此题的思路为:①先找出计算直角三角形内切圆半径的规律:半径r=$\frac{a+b+c}{2}$(a、b是直角边,c为斜边);②利用面积相等计算斜边上的高;③运用勾股定理计算直角三角形的边长.


科目:初中数学 来源: 题型:解答题
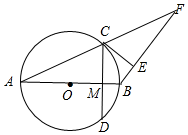 如图,以AB为直径的⊙O与AF交于C点,过C作CE⊥BF,且CE与⊙O相切,过C作CD⊥AB交AB于M,AB=10,OM:BM=3:2.
如图,以AB为直径的⊙O与AF交于C点,过C作CE⊥BF,且CE与⊙O相切,过C作CD⊥AB交AB于M,AB=10,OM:BM=3:2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
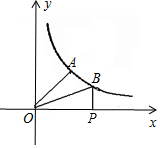 如图,已知A、B是反比例函数y=$\frac{k}{x}$图象上两点,BP⊥x轴,垂足为P.
如图,已知A、B是反比例函数y=$\frac{k}{x}$图象上两点,BP⊥x轴,垂足为P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某学校开展了以“人生观、价值观”为主题的班会活动,活动结束后,九年级某班一小组提出了5个主要观点并在本班50名学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图.
某学校开展了以“人生观、价值观”为主题的班会活动,活动结束后,九年级某班一小组提出了5个主要观点并在本班50名学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
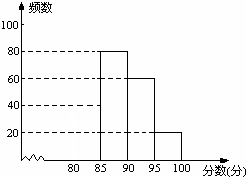 某校组织了一次环保知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题:
某校组织了一次环保知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题:| 分数段 | 频数 | 频率 |
| 80≤x<85 | a | 0.2 |
| 85≤x<90 | 80 | 0.4 |
| 90≤x<95 | 60 | b |
| 95≤x<100 | 20 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a+3a2=3a3 | B. | (a-b)2=a2-ab+b2 | C. | 2(a-b)=2a-2b | D. | (2ab)2÷ab=2ab |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com