
 上,作直线CD,ED,与直线AB分别交于点F,M,连接OC,求证:OC2=OM•OF;
上,作直线CD,ED,与直线AB分别交于点F,M,连接OC,求证:OC2=OM•OF; 上”改为“点D在
上”改为“点D在 上”,其余条件不变(如图②),
上”,其余条件不变(如图②),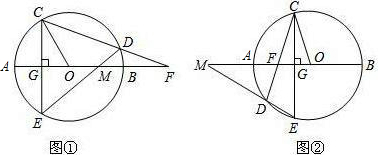 试问:(1)中的结论是否成立?并说明理由.
试问:(1)中的结论是否成立?并说明理由.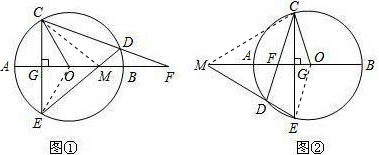 (1)证明:如图①,连接CM,OE,
(1)证明:如图①,连接CM,OE, ∠COE,∴∠AOC=∠CDE.
∠COE,∴∠AOC=∠CDE.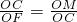 .
.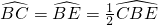 .
.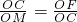 ,
, ∠COE,由圆周角定理知,∠AOC=∠CDE.由三角形的外角与内角的关系和等量代换求得∠OCM=∠F,故有△OMC∽△OCF,得到
∠COE,由圆周角定理知,∠AOC=∠CDE.由三角形的外角与内角的关系和等量代换求得∠OCM=∠F,故有△OMC∽△OCF,得到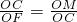 ,即OC2=OM•OF.
,即OC2=OM•OF.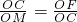 ,即OC2=OM•OF.
,即OC2=OM•OF.

科目:初中数学 来源: 题型:
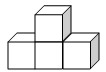 19、(1)画出如图所示几何体的主视图、左视图、俯视图.
19、(1)画出如图所示几何体的主视图、左视图、俯视图.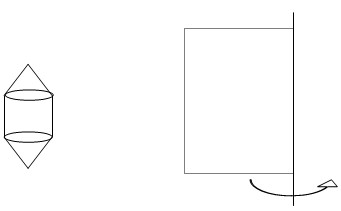
查看答案和解析>>
科目:初中数学 来源: 题型:
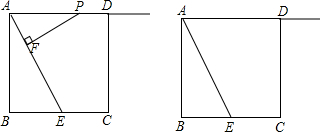 以P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,说明理由.
以P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
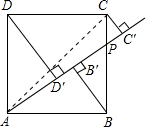 如图,正方形ABCD的边长为1,点P为边BC上任意一点(可与点B或点C重合),分别过点B、C、D作射线AP的垂线,垂足分别为点B′、C′、D′.求BB′+CC′+DD′的最大值和最小值.
如图,正方形ABCD的边长为1,点P为边BC上任意一点(可与点B或点C重合),分别过点B、C、D作射线AP的垂线,垂足分别为点B′、C′、D′.求BB′+CC′+DD′的最大值和最小值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com