
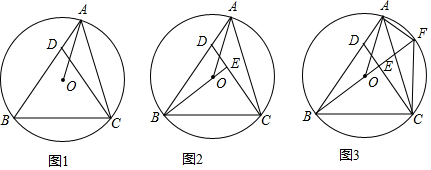
分析 (1)由等腰三角形的性质和三角形的外角性质证出∠AOC=2∠ABC,由圆周角定理证出∠ADC=∠AOC,再由对顶角相等和等腰三角形的性质即可得出结论;
(2)设∠OAB=∠OCD=x,由等腰三角形的性质得出∠OAB=∠OBA=x,由三角形的外角性质得出∠AOE=2x,再由直角三角形的性质和三角形的外角性质即可得出结论;
(3)过点C作CH⊥AF交AF的延长线于点H,连接CO并延长交AB于点S.证出四边形ASCH为矩形,由垂径定理得出AS=BS,由三角形中位线定理得出OS=$\frac{1}{2}$AF=$\frac{7}{4}$,设OB=OC=r,由勾股定理得出方程,解方程求出BS,即可得出△AFC的面积.
解答 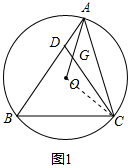 (1)证明:连接OC.如图1所示:
(1)证明:连接OC.如图1所示:
∵BD=CD,
∴∠DBC=∠DCB,∠ADC=2∠DBC,
∵∠AOC=2∠ABC,
∴∠ADC=∠AOC,
∵∠AGD=∠OGC,
∴∠BAO=∠GCO,
∵∠OCA=∠OCD+∠DAC,
∴∠OCA=∠OAB+∠ACD,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠OAC=∠OAB+∠ACD;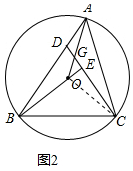
(2)证明:连接OC.如图2所示:
由(1)可知∠OAB=∠OCD,
设∠OAB=∠OCD=x,
∵OA=OB,
∴∠OAB=∠OBA=x,
∴∠AOE=2x,
∵BE⊥CD,
∴∠BEC=90°,
∴∠EOC=90°-x,
∴∠AOC=∠AOE+∠EOC=90°+x,
∵∠BOC=∠OCE+∠BEC=90°+x,
∴∠AOC=∠BOC
∵AC=BC; 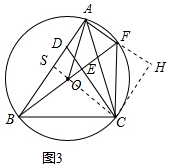
(3)解:过点C作CH⊥AF交AF的延长线于点H,连接CO并延长交AB于点S.如图3所示:
∵OB=OC,
∴∠OBC=∠OCB,
∵BD=CD,
∴∠DBC=∠DCB,
在△BCS和△CBE中,$\left\{\begin{array}{l}{∠DBC=∠DCB}&{\;}\\{BC=CB}&{\;}\\{∠OCB=∠OBC}&{\;}\end{array}\right.$,
∴△BCS≌△CBE(ASA),
∴∠BSC=∠CEB=90°,
∵BF为⊙O直径,
∴∠BAF=90°,
∵∠ASC=∠SAH=∠AHC=90°,
∴四边形ASCH为矩形,
∵OS⊥AB,
∴AS=BS,
∵OB=OF,
∴OS=$\frac{1}{2}$AF=$\frac{7}{4}$,
设OB=OC=r,∵AC=BC=10,
∴在Rt△OBS中 BS2=OB2-OS2,在Rt△CBS中 BS2=BC2-CS2,
∴OB2-OS2=BC2-CS2,
即r2-($\frac{7}{4}$)2=102-(r+$\frac{7}{4}$)2,
解得:r=$\frac{25}{4}$,或r=-8(舍去),
∴AS=BS=6,CS=8,
∵四边形ASCH为矩形,
∴AH=SC=8,CH=AS=BS=6,
∴△AFC的面积=$\frac{1}{2}$AF•CH=$\frac{1}{2}$×$\frac{7}{2}$×6=$\frac{21}{2}$.
点评 本题是圆的综合题目,考查了圆周角定理、垂径定理、等腰三角形的性质、三角形的外角性质、全等三角形的判定与性质、勾股定理、矩形的判定与性质等知识;本题综合性强,有一定难度.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 94,94 | B. | 94,95 | C. | 93,95 | D. | 93,96 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1+20%)a | B. | $\frac{a}{(1+20%)}$ | C. | 20%a | D. | $\frac{a}{20%}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
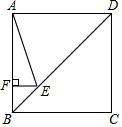 如果,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则BE的长为( )
如果,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则BE的长为( )| A. | 1 | B. | $\sqrt{2}$-1 | C. | 2$\sqrt{2}$-2 | D. | 4$\sqrt{2}$-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
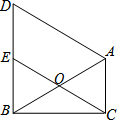 如图,在△ABC中,∠ACB=90°,∠ABC=30°.O为AB的中点,连接CO并延长到E,使OE=OC.过点A作AD∥CE交BE的延长线于D.
如图,在△ABC中,∠ACB=90°,∠ABC=30°.O为AB的中点,连接CO并延长到E,使OE=OC.过点A作AD∥CE交BE的延长线于D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两条对角线互相平分的四边形是平行四边形 | |
| B. | 两条对角线相等的菱形是正方形 | |
| C. | 两条对角线互相垂直的矩形是正方形 | |
| D. | 两条对角线相等的四边形是矩形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com