
如图,△ 为锐角三角形,△
为锐角三角形,△ 内接于圆
内接于圆 ,
, ,
, 是△
是△ 的垂心,
的垂心, 是
是 的直径.求证:
的直径.求证: .
.
见解析
【解析】
试题分析:易得△BCD为含30°的直角三角形,则CD=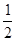 BD,利用H是垂心及直径所对的圆周角是直角可得四边形AHCD是平行四边形,则AH=CD,可得所证.
BD,利用H是垂心及直径所对的圆周角是直角可得四边形AHCD是平行四边形,则AH=CD,可得所证.
连接AD,CD,CH
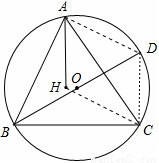
∵BD是⊙O直径,
∴∠BAD=∠BCD=90°,
又∠BAC=60°,
∴∠CAD=30°,∠DBC=∠CAD=30°,
在Rt△BCD中,CD=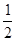 BD,H是△ABC的垂心,AH⊥BC,CH⊥AB,
BD,H是△ABC的垂心,AH⊥BC,CH⊥AB,
又DC⊥BC,DA⊥AB,
∴四边形AHCD为平行四边形,
∵AH=CD,
∴ .
.
考点:与圆有关的证明
点评:辅助线问题是初中数学的难点,能否根据题意准确作出适当的辅助线很能反映一个学生的对图形的理解能力,因而是中考的热点,尤其在压轴题中比较常见,需特别注意.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 如图,△ABC为锐角三角形,P,Q为边BC上的两点,△ABP和△ACQ的外接圆圆心分别为O1和O2.试判断BO1的延长线与CO2的延长线的交点D是否可能在△ABC的外接圆上,并说明理由.
如图,△ABC为锐角三角形,P,Q为边BC上的两点,△ABP和△ACQ的外接圆圆心分别为O1和O2.试判断BO1的延长线与CO2的延长线的交点D是否可能在△ABC的外接圆上,并说明理由.查看答案和解析>>
科目:初中数学 来源:2009-2010学年北京市101中学七年级下学期期末考试数学试卷(带解析) 题型:解答题
已知: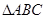 的高
的高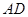 所在直线与高
所在直线与高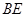 所在直线相交于点F。
所在直线相交于点F。
(1)如图①,若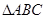 为锐角三角形,且
为锐角三角形,且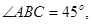 过点
过点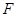 作
作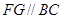 交直线
交直线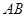 于点
于点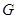 ,求证:
,求证: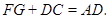
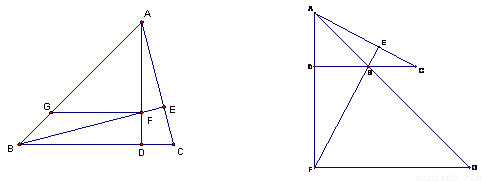
(2)如图②,若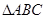 为钝角三角形,且
为钝角三角形,且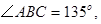 (1)中的其他条件不变,则
(1)中的其他条件不变,则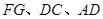 之间满足怎样的数量关系?并给出证明。
之间满足怎样的数量关系?并给出证明。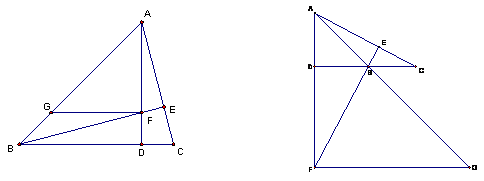
查看答案和解析>>
科目:初中数学 来源:2009-2010学年北京市七年级下学期期末考试数学试卷(解析版) 题型:解答题
已知: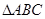 的高
的高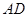 所在直线与高
所在直线与高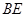 所在直线相交于点F。
所在直线相交于点F。
(1)如图①,若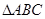 为锐角三角形,且
为锐角三角形,且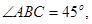 过点
过点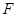 作
作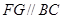 交直线
交直线 于点
于点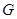 ,求证:
,求证: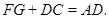
(2)如图②,若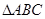 为钝角三角形,且
为钝角三角形,且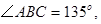 (1)中的其他条件不变,则
(1)中的其他条件不变,则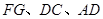 之间满足怎样的数量关系?并给出证明。
之间满足怎样的数量关系?并给出证明。
查看答案和解析>>
科目:初中数学 来源:《3.3 圆心角》2010年同步练习(解析版) 题型:解答题
 BD.
BD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com