
解:(1)∵c=-1,
∴直线y=

x-1,
当y=0时,

x-1=0,
解得x=2,
∴点A(2,0),
∵抛物线y=ax
2+bx+4c与y轴交于点C,c=-1,
∴点C(0,-4),
又∵点C为抛物线的顶点,
∴-

=0,
解得b=0,
把点A(2,0)代入抛物线解析式得,4a-4=0,
解得a=1,
所以,抛物线解析式为y=x
2-4,
联立

,
解得

(为点A坐标),

,
所以,点D(-

,-

);
(2)令y=0,则

x+c=0,解得x=-2c,
令x=0,则y=c,
所以,点A(-2c,0),B(0,c),
∵c>0,

∴OA=2c,OB=c,
根据勾股定理,AB=

=

=

c,
S
△ABC=

×

c×

=

×2c•c,
解得c=1,
∴OA=2,OB=1,AB=

,
又∵x=0时,y=4c=4×1=4,
∴点C坐标为(0,4),
∴OC=4,
∴AC=
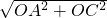
=

=2

,
∵∠CDB=∠ACB,∠CAB为公共角,
∴△ABC∽△ACD,
∴

=

,
即

=
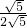
,
解得AD=4

,
过点D作DE⊥x轴于E,则△ABO∽△ADE,
∴
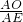
=

=
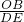
,
即
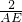
=

=
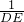
,
解得AE=8,DE=4,
∴OE=AE-OA=8-2=6,
∴点D(6,4),
∵抛物线y=ax
2+bx+4过点A(-2,0)、D(6,4),
∴

,
解得

,
所以,抛物线解析式为y=-

x
2+

x+4.
分析:(1)根据c的值确定出直线解析式,然后求出点A的坐标,再根据C为顶点可得b=0,然后把点A的坐标代入抛物线解析式求出a的值,再根据直线与抛物线解析式联立求解即可得到点D的坐标;
(2)根据直线解析式求出点A、B的坐标,从而得到OA、OB的长度,然后根据相似三角形对应边成比例列出比例式求出c=1,从而求出OA、OB、AB的长度,再根据勾股定理求出AB,根据∠CDB=∠ACB,∠CAB为公共角判定△ABC和△ACD相似,利用相似三角形对应边成比例列式求出AD的长度,过点D作DE⊥x轴于E,利用相似三角形对应边成比例求出AE、DE的长,再求出OE的长,然后得到点D的坐标,再利用待定系数法求二次函数解析式解答.
点评:本题是二次函数综合题型,主要涉及求直线与坐标轴的交点,待定系数法求函数解析式(包括二次函数解析式与一次函数解析式),联立两函数解析式求交点坐标,相似三角形的判定与性质,综合性较强,难度中等.

 x+c与x轴交于点A,与y轴交于点B,抛物线y=ax2+bx+4c与直线AB交于A、D两点,与y轴交于点C.
x+c与x轴交于点A,与y轴交于点B,抛物线y=ax2+bx+4c与直线AB交于A、D两点,与y轴交于点C. ,∠CDB=∠ACB,求抛物线的解析式.
,∠CDB=∠ACB,求抛物线的解析式. 解:(1)∵c=-1,
解:(1)∵c=-1, x-1,
x-1, x-1=0,
x-1=0, =0,
=0, ,
, (为点A坐标),
(为点A坐标), ,
, ,-
,- );
); x+c=0,解得x=-2c,
x+c=0,解得x=-2c,
 =
= =
= c,
c, ×
× c×
c× =
= ×2c•c,
×2c•c, ,
,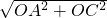 =
= =2
=2 ,
, =
= ,
, =
=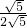 ,
, ,
,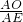 =
= =
=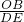 ,
,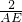 =
= =
=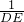 ,
, ,
, ,
, x2+
x2+ x+4.
x+4.

 已知:直线y=-2x+4交x轴于点A,交y轴于点B,点C为x轴上一点,AC=1,且OC<OA.抛物线y=ax2+bx+c(a≠0)经过点A、B、C.
已知:直线y=-2x+4交x轴于点A,交y轴于点B,点C为x轴上一点,AC=1,且OC<OA.抛物线y=ax2+bx+c(a≠0)经过点A、B、C. 已知:直线y=kx+b的图象过点A(-3,1);B(-1,2),
已知:直线y=kx+b的图象过点A(-3,1);B(-1,2),