Question

巳知y=y₁+y₂，y₁与x-1成正比例，y₂与x成反比例，并且x=1时y=2，x=2时y=3，求x=4时y的值．

Answer 1

解：∵y₁与x成正比例，y₂与x成反比例，
∴y₁=kx，y₂=．
∵y=y₁+y₂，
∴y=kx+，
∵当x=1时，y=2；当x=2时，y=3，
∴2=k+m，3=2k+，
解得k=，m=．
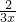
∴y=x-，即当x=4时，y=．
分析：首先根据题意，分别表示出应表示出y₁与x，y₂与x的函数关系式，再进一步表示出y与x的函数关系式；然后根据已知条件，得到方程组，即可求解．
点评：本题考查函数值的知识，解决本题的关键是得到y与x的函数关系式，需注意两个函数的比例系数是不同的．