
����Ŀ����֪����ʽ2x3y��xy+16�Ĵ���Ϊa��������Ϊb��a��b�ֱ��Ӧ�������ϵ�A��B���㣮
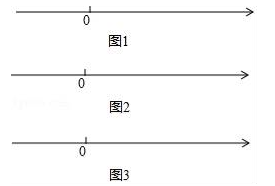
��1��a= ��b= �����������ϻ���A��B���㣻
��2������P�ӵ�A��������ÿ��3����λ���ȵ�λ���ٶ���x���������˶������˶�ʱ��Ϊ����ʱ����P����A�ľ����ǵ�P����B�ľ����2����
��3�������ϻ���һ��C������Ϊ30������P��Qͬʱ�ӵ�A�͵�B�������ֱ���ÿ��3����λ���Ⱥ�ÿ��1����λ���ȵ��ٶ���C���˶���P����C�����������ͬ�����ٶȷ��أ��˶����յ�A�����P�͵�Q�˶�������ʱ��P��Q����֮��ľ���Ϊ4���������ʱ��Q�����꣮
���𰸡���1��4��16����2��![]() ��8�룻��3����P�͵�Q�˶���4��8��9��11��ʱ��P��Q����֮��ľ���Ϊ4��
��8�룻��3����P�͵�Q�˶���4��8��9��11��ʱ��P��Q����֮��ľ���Ϊ4��
�������������������1�����ݶ���ʽ�Ĵ�������������Ķ���Ϳ��Եó����ۣ��Ϳ������A��B����ʾ�����������������ϱ�ʾ���ɣ�
��2�����˶�ʱ��Ϊts�������⣺3t=2��16��4��3t����3t=2��4+3t��16�����ⷽ�̼��ɵ���
��3�����˶�ʱ��Ϊts�������⣺12+t��3t=4��3t����12+t��=4��12+t+4+3t=52��12+t+3t��4=52���ⷽ�̼��ɵ�.
�����������1���߶���ʽ2x3y��xy+16�Ĵ���Ϊa��������Ϊ b��
��a=4��b=16��
�ʴ�Ϊ4��16��
��A��B��λ����ͼ��ʾ��
![]()
��2�����˶�ʱ��Ϊts��
�����⣺3t=2��16��4��3t����3t=2��4+3t��16����
���t=![]() ��8��
��8��
���˶�ʱ��Ϊ![]() ��8��ʱ���� P����A�ľ����ǵ�P����B�ľ����2����
��8��ʱ���� P����A�ľ����ǵ�P����B�ľ����2����
��3�����˶�ʱ��Ϊts��
�����⣺12+t��3t=4��3t����12+t��=4��12+t+4+3t=52��12+t+3t��4=52��
���t=4��8��9��11��
���P�͵�Q�˶�ʱ��Ϊ4��8��9��11��ʱ��P��Q����֮��ľ���Ϊ4��


 �ŵ������ϵ�д�
�ŵ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������C1��y=x2����ƽ��2����λ���ȣ�������ƽ��3����λ���ȵõ�������C2 �� ��������C2��Ӧ�ĺ�������ʽ�ǣ� ��
A.y=��x��2��2��3
B.y=��x+2��2��3
C.y=��x��2��2+3
D.y=��x+2��2+3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�߲˾�Ӫ�����߲������г������߲˽������ۣ������߲������۸������ۼ۸������
�߲�Ʒ�� | ������ | �ཷ | ������ | ���� |
�����ۣ�Ԫ/�K�� | 3.6 | 5.4 | 8 | 4.8 |
���ۼۣ�Ԫ/�K�� | 5.4 | 8.4 | 14 | 7.6 |
�����������⣺
��1����һ�죬�þ�Ӫ�������������������������߲˹�300�K����ȥ��1520ԪǮ���������߲˵���ȫ������һ���˶���ԪǮ��
��2���ڶ��죬�þ�Ӫ����1520Ԫ��Ȼ��������������������Ҫ�뵱��ȫ���������Ǯ��������1050Ԫ����þ�Ӫ��������������������٩K��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
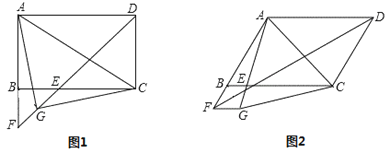
����Ŀ����![]() ABCD�У���ADC��ƽ���߽�ֱ��BC�ڵ�E����AB���ӳ����ڵ�F������AC.
ABCD�У���ADC��ƽ���߽�ֱ��BC�ڵ�E����AB���ӳ����ڵ�F������AC.
��1����ͼ1������ADC=90�㣬G��EF���е㣬����AG��CG.
����֤��BE=BF��
�����жϡ�AGC����״����˵������.
��2����ͼ2������ADC=60�㣬���߶�FB�Ƶ�F˳ʱ����ת60����FG������AG��CG���жϡ�AGC����״.��ֱ��д�����۲���֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2����m+3��x+m=0��
��1����֤������ʵ��mȡ��ֵ������������������ȵ�ʵ������
��2��������һ������2����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�E����ACƽ�֡�DAB����AB��AC��AC��AD���������ĸ����ۣ���AC��BD����BC��DE���ۡ�DBC����DAC���ܡ�ABC���������Σ���д����ȷ���۵������������Ϊ��ȷ���۵���Ŷ����ϣ�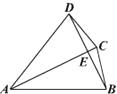
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A(3����1)����ԭ��ĶԳƵ�A���������( )
A. (��3����1) B. (3��1) C. (��3��1) D. (��1��3)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AD�ǡ�A�����ƽ���ߣ�P��AD������A������һ�㣬��PB=m��PC=n��AB=c��AC=b����m+n���루b+c���Ĵ�С��ϵ�ǣ� �� 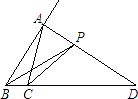
A.m+n��b+c
B.m+n��b+c
C.m+n=b+c
D.��ȷ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com