
如图,∠C=90º,点A、B在∠C的两边上,CA=30,CB=20,连接AB.点P从点B出发,以每秒4个单位长度的速度沿BC的方向运动,到点C停止.当点P与B、C两点不重合时,作PD⊥BC交AB于点D,作DE⊥AC于点E.F为射线CB上一点,使得∠CEF=∠ABC.设点P运动的时间为x秒.
【小题1】用含有x的代数式表示CE的长
【小题2】求点F与点B重合时x的值
【小题3】当点F在线段CB上时,设四边形DECP与四边形DEFB重叠部分图形的面积为y(平方单位).求y与x之间的函数关系式
科目:初中数学 来源: 题型:
如图![]() △
△![]() 中,∠
中,∠![]() =90°,
=90°,![]() =4,
=4,![]() =5,点
=5,点![]() 是
是![]() 上的一个动点(
上的一个动点(![]() 不与点
不与点![]() 、点
、点![]() 重合),PQ⊥
重合),PQ⊥![]() ,垂足为Q,当PQ与△
,垂足为Q,当PQ与△![]() 的内切圆⊙O相切时,
的内切圆⊙O相切时, 的值为( ▲ )
的值为( ▲ )
A.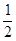 B.1 C.
B.1 C.![]() D.
D.![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,∠MON=90°,AP平分∠MAB,BP平分∠ABN.

(1)求∠P的度数;
(2)若∠MON=80°,其余条件不变,求∠P的度数;
(3)经过(1)、(2)的计算,猜想并证明∠MON与∠P的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
 △
△ 中,∠
中,∠ =90°,
=90°, =4,
=4, =5,点
=5,点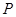 是
是 上的一个动点(
上的一个动点(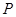 不与点
不与点 、点
、点 重合),PQ⊥
重合),PQ⊥ ,垂足为Q,当PQ与△
,垂足为Q,当PQ与△ 的内切圆⊙O相切时,
的内切圆⊙O相切时, 的值为( ▲ )
的值为( ▲ )A. | B.1 | C. | D. |

查看答案和解析>>
科目:初中数学 来源: 题型:
| A.ΔPAB∽ΔPDA | B.ΔABC∽ΔDCA |
| C.ΔPAB∽ΔPCA | D.ΔABC∽ΔDBA |

查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省桐乡市九年级上学期基础调研数学试卷(解析版) 题型:选择题
如图,∠XOY=90°,OW平分∠XOY,PA⊥OX,PB⊥OY,PC⊥OW.若OA+OB+OC=1,则OC=( )

(A)2- (B)
(B) -1 (C)6-
-1 (C)6- (D)
(D) -3
-3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com