
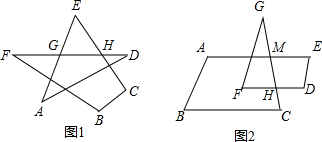
 (1)如图1,求∠A+∠B+∠C+∠D+∠E+∠F的度数;
(1)如图1,求∠A+∠B+∠C+∠D+∠E+∠F的度数;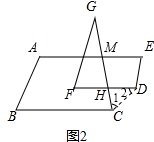 (2)如图,连接CD.
(2)如图,连接CD.

科目:初中数学 来源: 题型:
| AC |
| OF |
| AC |
| OF |
查看答案和解析>>
科目:初中数学 来源: 题型:
 学校举行元旦晚会,在操场上搭建一个半径为8m的圆形舞台,在舞台的中心O点的上方安装了一个照明光源S,S射到地面上的光束成锥形,其轴截面SAB的顶角为120°(如图),求光源距地面的垂直高度SO和光束构成的锥形的侧面积.(精确到0.1m)
学校举行元旦晚会,在操场上搭建一个半径为8m的圆形舞台,在舞台的中心O点的上方安装了一个照明光源S,S射到地面上的光束成锥形,其轴截面SAB的顶角为120°(如图),求光源距地面的垂直高度SO和光束构成的锥形的侧面积.(精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com