
 如图,抛物线y=ax2+bx-a-b(a<0,a、b为常数)与x轴交于A、C两点,与y轴交于B点,直线AB的函数关系式为y=$\frac{8}{9}$x+$\frac{16}{3}$.
如图,抛物线y=ax2+bx-a-b(a<0,a、b为常数)与x轴交于A、C两点,与y轴交于B点,直线AB的函数关系式为y=$\frac{8}{9}$x+$\frac{16}{3}$.分析 (1)根据已知条件得到B(0,$\frac{16}{3}$),A(-6,0),解方程组得到抛物线的函数关系式为:y=-$\frac{8}{9}$x2-$\frac{40}{9}$x+$\frac{16}{3}$,于是得到C(1,0);
(2)由点M(m,0),过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点,得到D(m,$\frac{8}{9}$m+$\frac{16}{3}$),当DE为底时,作BG⊥DE于G,根据等腰三角形的性质得到EG=GD=$\frac{1}{2}$ED,GM=OB=$\frac{16}{3}$,列方程即可得到结论;
(3)i:根据已知条件得到ON=OM′=4,OB=$\frac{16}{3}$,由∠NOP=∠BON,特殊的当△NOP∽△BON时,根据相似三角形的性质得到$\frac{OP}{ON}=\frac{NP}{NB}=\frac{ON}{OB}$=$\frac{3}{4}$,于是得到结论;
ii:根据题意得到N在以O为圆心,4为半径的半圆上,由(i)知,$\frac{NP}{NB}=\frac{OP}{ON}$=$\frac{3}{4}$,得到NP=$\frac{3}{4}$NB,于是得到(NA+$\frac{3}{4}$NB)的最小值=NA+NP,此时N,A,P三点共线,根据勾股定理得到结论.
解答 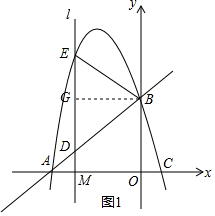 解:(1)在y=$\frac{8}{9}$x+$\frac{16}{3}$中,令x=0,则y=$\frac{16}{3}$,令y=0,则x=-6,
解:(1)在y=$\frac{8}{9}$x+$\frac{16}{3}$中,令x=0,则y=$\frac{16}{3}$,令y=0,则x=-6,
∴B(0,$\frac{16}{3}$),A(-6,0),
把B(0,$\frac{16}{3}$),A(-6,0)代入y=ax2+bx-a-b得$\left\{\begin{array}{l}{36a-6b-a-b=0}\\{-a-b=\frac{16}{3}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=-\frac{8}{9}}\\{b=-\frac{40}{9}}\end{array}\right.$,
∴抛物线的函数关系式为:y=-$\frac{8}{9}$x2-$\frac{40}{9}$x+$\frac{16}{3}$,
令y=0,则=-$\frac{8}{9}$x2-$\frac{40}{9}$x+$\frac{16}{3}$=0,
∴x1=-6,x2=1,
∴C(1,0);
(2)∵点M(m,0),过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点,
∴D(m,$\frac{8}{9}$m+$\frac{16}{3}$),当DE为底时,
作BG⊥DE于G,则EG=GD=$\frac{1}{2}$ED,GM=OB=$\frac{16}{3}$,
∵DM+DG=GM=OB,
∴$\frac{8}{9}$m+$\frac{16}{3}$$+\frac{1}{2}$(-$\frac{8}{9}$m2-$\frac{40}{9}$m+$\frac{16}{3}$-$\frac{8}{9}$m-$\frac{16}{3}$)=$\frac{16}{3}$,
解得:m1=-4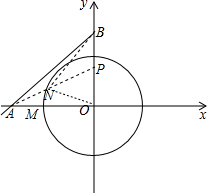 ,m2=0(不合题意,舍去),
,m2=0(不合题意,舍去),
∴当m=-4时,△BDE恰好是以DE为底边的等腰三角形;
(3)i:存在,
∵ON=OM′=4,OB=$\frac{16}{3}$,
∵∠NOP=∠BON,
∴当△NOP∽△BON时,$\frac{OP}{ON}=\frac{NP}{NB}=\frac{ON}{OB}$=$\frac{3}{4}$,
∴$\frac{NP}{NB}$不变,
即OP=$\frac{3}{4}$ON=$\frac{3}{4}$×4=3,
∴P(0,3)
ii:∵N在以O为圆心,4为半径的半圆上,由(i)知,$\frac{NP}{NB}=\frac{OP}{ON}$=$\frac{3}{4}$,
∴NP=$\frac{3}{4}$NB,
∴(NA+$\frac{3}{4}$NB)的最小值=NA+NP,
∴此时N,A,P三点共线,
∴(NA+$\frac{3}{4}$NB)的最小值=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$.
点评 本题考查了待定系数法求函数的解析式,等腰三角形的性质,相似三角形的性质,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 水龙头关闭不严会造成滴水,为了调查漏水量与漏水时间的关系,进行以下实验:在滴水的水龙头下放置一个能显示水量的容器,每5min记录一次容器的水量,记录数据如下表:
水龙头关闭不严会造成滴水,为了调查漏水量与漏水时间的关系,进行以下实验:在滴水的水龙头下放置一个能显示水量的容器,每5min记录一次容器的水量,记录数据如下表:| 时间 (分钟) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| 水量 (毫升) | 0 | 50 | 90 | 150 | 210 | 250 | 300 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1=y2 | B. | y1>y2 | C. | y1<y2 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月销量y(个) | 100 | 160 | 240 | 320 |
| 每个工具的固定成本Q(元) | 96 | 60 | 40 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
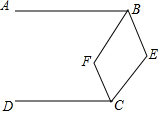 如图,AB∥CD,E为直线BC右侧一点,连接BE、CE,作∠ABE和∠DCE的角平分线BF、CF相交于点F.
如图,AB∥CD,E为直线BC右侧一点,连接BE、CE,作∠ABE和∠DCE的角平分线BF、CF相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com