已知样本x1,x2,x3,…,xn的方差是1,那么样本2x1+3,2x2+3,2x3+3,…,2xn+3的方差是( )
A.1
B.2
C.3
D.4
【答案】
分析:根据方差的意义分析,数据都加3,方差不变,原数据都乘2,则方差是原来的4倍.
解答:解:设样本x
1,x
2,x
3,…,x
n的平均数为m,
则其方差为S
12=
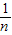
[(x
1-m)
2+(x
2-m)
2+…+(x
n-m)
2]=1,
则样本2x
1+3,2x
2+3,2x
3+3,…,2x
n+3的平均数为2m,其方差为S
22=4S
12=4.
故选D.
点评:本题考查方差的计算公式及其运用:一般地设有n个数据,x
1,x
2,…x
n,若每个数据都放大或缩小相同的倍数后再同加或同减去一个数,其平均数也有相对应的变化,方差则变为这个倍数的平方倍.
