练习册

  • 练习册
  • 试题
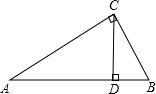
    精英家教网 > 初中数学 > 题目详情
    精英家教网已知：如图在Rt△ABC中，∠C=90°，CD为AB边上的高，△ABC的周长为24，BC：AC=3：4，求CD的长及△ABC的面积．
    分析：根据题意设BC的长为3a，根据勾股定理可以求出AB的长为5a，根据周长求出三边长，再根据面积公式可以求出CD的长和三角形的面积．
    解答：解：设BC的长为3a，则AC的长为4a
    根据勾股定理：AB2=BC2+AC2
    ∴AB=5a
    ∵C△ABC=AB+BC+AC=24
    ∴AB=10，BC=6，AC=8
    S△ABC=
    1
    2
    AC•BC=
    1
    2
    AB•CD    =24
    ∴CD=4.8．
    点评：本题考查的是三角形面积公式和勾股定理的灵活运用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网已知：如图在Rt△ABC和Rt△BAD中，AB为斜边，AC=BD，BC与AD相交于点E．
    求证：AE=BE．

    查看答案和解析>>

    科目：初中数学 来源：2013-2014学年山东青岛市崂山区九年级第一学期期末考试数学试卷（解析版） 题型：解答题

    已知：如图①,在Rt△ACB中,∠C＝90º,AC＝6cm,BC＝8cm,点P由B出发沿BC方向向点C匀速运动,速度为2cm/s；点Q由A出发沿AB方向向点B匀速运动,速度为1cm/s；连接PQ．若设运动的时间为t(s)（0＜t＜4）,解答下列问题：

    （1）当t为何值时,PQ的垂直平分线经过点B？

    （2）如图②,连接CQ．设△PQC的面积为y（cm2）,求y与t之间的函数关系式；

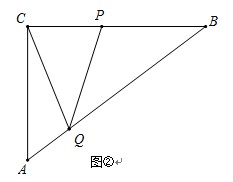
    （3）如图②,是否存在某一时刻t,使线段C Q恰好把四边形ACPQ的面积分成1：2的两部分？若存在,求出此时t的值；若不存在,说明理由.

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    已知：如图在Rt△ABC中，∠C=90°，CD为AB边上的高，△ABC的周长为24，BC：AC=3：4，求CD的长及△ABC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：如图在Rt△ABC中，斜边AB＝5厘米，BC＝厘米，AC＝b厘米，＞b，且、b是方程的两根。

    ⑴ 求和b的值；

    ⑵ 与开始时完全重合，然后让固定不动，将以1厘米/秒的速度沿所在的直线向左移动。

    ① 设x秒后与的重叠部分的面积为y平方厘米，

    求y与x之间的函数关系式,并写出x的取值范围；

    ② 几秒后重叠部分的面积等于平方厘米？

    查看答案和解析>>

    同步练习册答案