
如图,以△
ABC的边AB为直径的⊙O交AC边于点D,且过点D的切线DE平分BC边.
(1)BC与⊙O是否相切?请说明理由;
(2)当△ABC满足什么条件时,以点O、B、E、D为顶点的四边形是平行四边形?并说明理由.
|
分析: (1)要判断BC与⊙O是否相切,只需判断∠ABC是否等于90°;(2)可进行逆向思维:若四边形OBED是平行四边形,则应有OD∥BC.由(1)知∠ABC=90°,所以∠AOD=90°.而OA=OD,所以∠A=∠ADO=45°,从而可得△ABC为等腰直角三角形.解: (1)BC与⊙O相切.理由:连接 OD、BD.因为 DE切⊙O于点D,AB为直径,所以∠EDO=∠ADB=90°.因为 DE平分CB,所以DE=又因为∠ ODB=∠OBD,∠ODB+∠EDB=90°,所以∠OBD+∠EBD=90°,即∠ABC=90°.所以BC与⊙O相切.(2)当△ABC为等腰直角三角形(∠ABC=90°)时,四边形OBED是平行四边形. 理由:因为△ ABC是等腰直角三角形(∠ABC=90°),所以AB=BC.因为 BD⊥AC于点D,所以D为AC的中点.所以OD=所以四边形 OBED是平行四边形. |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 26、如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形.
26、如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:
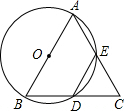 如图,以△ABC的边AB为直径作⊙O,交BC于D点,交AC于E点,BD=DE
如图,以△ABC的边AB为直径作⊙O,交BC于D点,交AC于E点,BD=DE | BD |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2011•峨眉山市二模)如图,以△ABC的边AB为直径作⊙O,BC与⊙O交于D,D是BC的中点,过D作DE⊥AC,交AC于点E.
(2011•峨眉山市二模)如图,以△ABC的边AB为直径作⊙O,BC与⊙O交于D,D是BC的中点,过D作DE⊥AC,交AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2010•黔东南州)如图,以△ABC的边BC为直径作⊙O分别交AB,AC于点F.点E,AD⊥BC于D,AD交于⊙O于M,交BE于H.
(2010•黔东南州)如图,以△ABC的边BC为直径作⊙O分别交AB,AC于点F.点E,AD⊥BC于D,AD交于⊙O于M,交BE于H.查看答案和解析>>
科目:初中数学 来源: 题型:
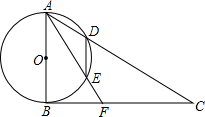 如图,以△ABC的边AB为直径的⊙O交AC于点D,弦DE∥AB,∠C=∠BAF
如图,以△ABC的边AB为直径的⊙O交AC于点D,弦DE∥AB,∠C=∠BAF| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com