
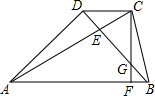
 如图,梯形ABCD中,AB∥CD,△ABD为等腰直角三角形,∠ADB=90゜,AC=AB,AC与BD相交于E点,CF⊥AB于点F,交BD于G点.下列结论:
如图,梯形ABCD中,AB∥CD,△ABD为等腰直角三角形,∠ADB=90゜,AC=AB,AC与BD相交于E点,CF⊥AB于点F,交BD于G点.下列结论: AB;②BE=BC;③BC=
AB;②BE=BC;③BC= CD;④CE=2BF,
CD;④CE=2BF, AB,易得四边形DHFC是矩形,即可证得CF=
AB,易得四边形DHFC是矩形,即可证得CF= AB;
AB; AB,AC=AB,易得∠CAB=30°,又由AC=AB,易求得∠BCE=∠BEC=75°,则可得BE=BC;
AB,AC=AB,易得∠CAB=30°,又由AC=AB,易求得∠BCE=∠BEC=75°,则可得BE=BC; AB;
AB; AB,故正确.
AB,故正确. AB,AC=AB,
AB,AC=AB, AC,
AC,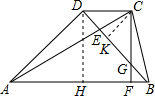 ∴BE=BC.故正确;
∴BE=BC.故正确; CD,
CD, CD,故正确.
CD,故正确.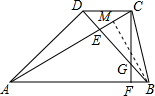 ④直角△CBF中,∠BCF=90°-75°=15°,
④直角△CBF中,∠BCF=90°-75°=15°, CE,∠CBM=
CE,∠CBM= ∠CBE=15°,
∠CBE=15°,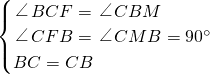
 CE,
CE,

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
 如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,cosC=
如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,cosC=
| ||
| 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com