Question

已知直线y=kx-1与x轴、y轴分别交于点A、点B，O为坐标原点，k＜0，∠BAO=30°．以线段AB为边在第三象限内作等边△ABC．
（1）求出k的值；
（2）求出点C的坐标；
（3）若在第三象限内有一点P（m，），且△ABP的面积和△ABC的面积相等，求m的值．

Answer 1

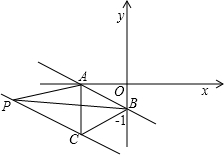
解：（1）对于直线y=kx-1，令x=0，解得y=-1，
则B（0，-1），即OB=1，
∵∠BAO=30°，
∴在Rt△OAB中，AB=2OB=2，
根据勾股定理得：OA==，
∵k＜0，
∴A（-，0），
把A（-，0）代入y=kx-1中得：k=-；

（2）∵AB=2，∠BAO=30°，△ABC为等边三角形，
∴AB=AC=2，∠OAC=∠BAO+∠BAC=30°+60°=90°，
∵C在第三象限，OA=，
∴C（-，-2）；

（3）∵△ABP的面积和△ABC的面积相等，
∴直线PC∥直线AB，
设直线PC解析式为y=-x+b，
把C（-，-2）代入直线PC得：-2=-×（-）+b，即b=-3，
∴直线PC解析式为y=-x-3，
把点P（m，-）代入直线PC，得-=-m-3，
解得：m=-．
分析：（1）对于直线y=kx-1，令x=0求出y=-1，可得出B坐标为（0，-1），进而确定出OB的长，在直角三角形AOB中，由∠BAO=30°，利用30°所对的直角边等于斜边的一半得到AB=2OB，求出AB的长，利用勾股定理求出OA的长，由k小于0，确定出A的坐标，将A坐标代入直线y=kx-1中，即可求出k的值；
（2）由三角形ABC为等边三角形，得到∠BAC为60°，由∠BAO+∠BAC得到∠OAC为直角，再由AB的长，求出AC的长，即为C纵坐标的绝对值，OA为C横坐标的绝对值，由C为第三象限点，即可确定出C的坐标；
（3）由三角形ABP的面积与三角形ABC的面积相等，且AB为两三角形的公共边，得到AB边上的高相等，进而得到直线PC与直线AB平行，即两直线的斜率相等，由直线AB的斜率设出直线PC的解析式为y=-x+b，将C坐标代入求出b的值，确定出直线PC解析式，将P坐标代入直线PC解析式中，即可求出m的值．
点评：此题考查了一次函数综合题，涉及的知识有：坐标与图形性质，含30度直角三角形的性质，等边三角形的性质，待定系数法确定一次函数解析式，平行线的性质，以及勾股定理，熟练掌握性质及定理是解本题的关键．