解:(1)∵AB=AC,AD=AE,B、A、E在同一条直线上,C、A、D在同一条直线上,
∴BE=CD,
而PB=PD,PC=PE,
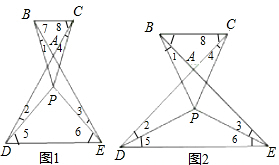
∴△BPE≌△DPC,
∴∠1=∠2,∠3=∠4,
∵∠BAC=60°,
∴△ABC和△ADE为等边三角形,
∴∠7=∠8=∠2+∠5=∠3+∠6=60°,
∵∠BPC=180°-∠1-∠4-∠7-∠8=60°-∠1-∠4;∠DPE=180°-∠5-∠6=180°-(60°-∠2)-(60°-∠3)=60°+∠2+∠3,
∴∠BPC+∠DPE=60°×2=120°;
(2)同理可证得∠1=∠2,∠3=∠4,
∵∠BAC=90°,
∴∠7=∠8=∠2+∠5=∠3+∠6=45°,
∴∠BPC=180°-∠1-∠4-∠7-∠8=90°-∠1-∠4,
∠DPE=180°-∠5-∠6=180°-(45°-∠2)-(45°-∠3)=90°+∠2+∠3,
∴∠BPC+∠DPE=180°;
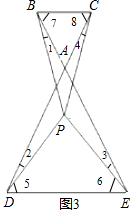
故答案为120°,180°.
(3)由(1)可得∠1=∠2,∠3=∠4,
∵∠BAC=α,而AB=AC,PD=PE,
∴∠7=∠8=∠2+∠5=∠3+∠6=90°-

α,
∴∠BPC=180°-∠1-∠4-∠7-∠8=α-∠1-∠4,
∠DPE=180°-∠5-∠6=180°-(90°-

α
-∠2)-(90°-

α
-∠3)=α+∠2+∠3,
∴∠BPC+∠DPE=2α.
分析:(1)先易证得△BPE≌△DPC,得到∠1=∠2,∠3=∠4,由∠BAC=60°,得到△ABC和△ADE为等边三角形,则∠7=∠8=∠2+∠5=∠3+∠6=60°,根据三角形的内角和定理得到∠BPC=180°-∠1-∠4-∠7-∠8=60°-∠1-∠4,∠DPE=180°-∠5-∠6=180°-(60°-∠2)-(60°-∠3)=60°+∠2+∠3,即可得到∠BPC+∠DPE;
(2)同一样,只是∠BAC=90°,得到∠7=∠8=∠2+∠5=∠3+∠6=45°,则∠BPC=180°-∠1-∠4-∠7-∠8=90°-∠1-∠4,∠DPE=180°-∠5-∠6=180°-(45°-∠2)-(45°-∠3)=90°+∠2+∠3,即可得到∠BPC+∠DPE;
(3)同前面的证法一样,由∠BAC=α,而AB=AC,PD=PE,得到∠7=∠8=∠2+∠5=∠3+∠6=90°-

α,即可得到∠BPC+∠DPE=2α;
点评:本题考查了等腰三角形的性质:已知等腰三角形的顶角根据三角形的内角和定理可得到底角的度数.也考查了三角形全等的判定与性质以及等边三角形和等腰直角三角形的性质.

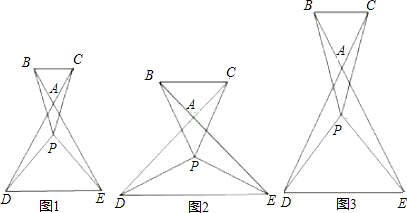


 α,
α, α
α α
α α,即可得到∠BPC+∠DPE=2α;
α,即可得到∠BPC+∠DPE=2α;

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案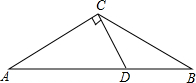 如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D.
如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D. 如图,已知在等腰△ABC中,∠ACB=120°.
如图,已知在等腰△ABC中,∠ACB=120°.