Question

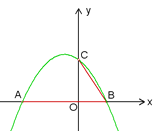
【题目】如图1，抛物线y＝－x2－x＋3与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C．（1）求点A、B的坐标；（2）设D为已知抛物线的对称轴上的任意一点，当△ACD的面积等于△ACB的面积时，求点D的坐标；（3）若直线l过点E（4, 0），M为直线l上的动点，当以A、B、M为顶点所作的直角三角形有且只有三个时，求直线l的解析式．

Answer 1

【答案】（1）A（－4， 0）B（2， 0）；（2）（1，）,；（3）y＝x－3

【解析】

试题分析：（1）根据二次函数当y=0时得出A、B两点的坐标；（2）△ACD与△ACB有公共的底边AC，当△ACD的面积等于△ACB的面积时，点B、D到直线AC的距离相等．过点B作AC的平行线交抛物线的对称轴于点D，在AC的另一侧有对应的点D′，根据三角形相似得出点的坐标；（3）过点A、B分别作x轴的垂线，这两条垂线与直线l总是有交点的，即2个点M．以AB为直径的⊙G如果与直线l相交，那么就有2个点M；如果圆与直线l相切，就只有1个点M了，根据Rt△EGM得出EM的长度，从而得出点的坐标，然后求出函数解析式.

试题解析：（1）由函数解析式可得交点坐标为A（－4， 0）B（2， 0）．

（2）△ACD与△ACB有公共的底边AC，当△ACD的面积等于△ACB的面积时，点B、D到直线AC的距离相等．

过点B作AC的平行线交抛物线的对称轴于点D，在AC的另一侧有对应的点D′．

设抛物线的对称轴与x轴的交点为G，与AC交于点H．

由BD//AC，得∠DBG＝∠CAO．∴

∴，点D的坐标为

∵AC//BD，AG＝BG，∴HG＝DG．

而D′H＝DH，

∴D′G＝3DG．

∴D′的坐标为

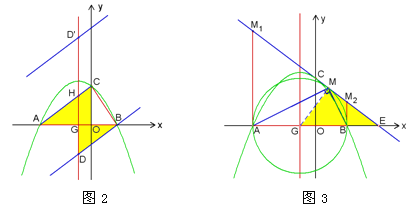
（3）过点A、B分别作x轴的垂线，这两条垂线与直线l总是有交点的，即2个点M．

以AB为直径的⊙G如果与直线l相交，那么就有2个点M；如果圆与直线l相切，就只有1个点M了．

连接GM，那么GM⊥l．

在Rt△EGM中，GM＝3，GE＝5，所以EM＝4．

在Rt△EM1A中，AE＝8，，所以M1A＝6

∴点M1的坐标为（－4， 6），过M1、E的直线l为y＝－x＋3．

根据对称性，直线l还可以是y＝x－3．