
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
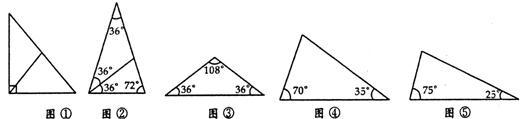
 如图所示,顶角为36°的等腰三角形,其底边与腰之比等于k,这样的三角形叫黄金三角形,已知腰长AB=1,△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形,以此类推,第2007个黄金三角形的周长为( )
如图所示,顶角为36°的等腰三角形,其底边与腰之比等于k,这样的三角形叫黄金三角形,已知腰长AB=1,△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形,以此类推,第2007个黄金三角形的周长为( )| A、k2006 | ||
| B、k2007 | ||
C、
| ||
| D、k2006(2+k) |
查看答案和解析>>
科目:初中数学 来源: 题型:
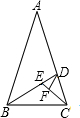
 20、已知:△ABC与△CDE都是顶角为36°的等腰三角形,BC=CD,AC与BD交于F,且B、C、E三点共线.
20、已知:△ABC与△CDE都是顶角为36°的等腰三角形,BC=CD,AC与BD交于F,且B、C、E三点共线.查看答案和解析>>
科目:初中数学 来源: 题型:
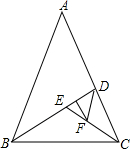 如图所示,顶角为36°的等腰三角形,其底边与腰之比等于k,这样的三角形叫做黄金三角形.已知AB=1,△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形,以此类推,第2014个黄金三角形的周长为( )
如图所示,顶角为36°的等腰三角形,其底边与腰之比等于k,这样的三角形叫做黄金三角形.已知AB=1,△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形,以此类推,第2014个黄金三角形的周长为( )查看答案和解析>>
科目:初中数学 来源:2011年河北省中考考前模拟测试数学卷(3) 题型:解答题
我们知道:直角三角形斜边上的中线等于斜边的一半,说明斜边上的中线可把直角三角形分成两个等腰三角形(图①)。又比如,顶角为36°的等腰三角形也能分成两个等腰三角形(图②)。
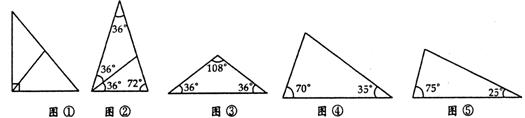
1.试试看,你能把图③、图④、图⑤中的三角形分成两个等腰三角形吗
2.△ABC中,有一内角为36°,过某一顶点的直线将△ABC分成两个等腰三角形,则满足上述条件的不同形状(相似的认为是同一形状)的△ABC最多有5种,除了图②、图③中的两种,还有三种,请你画出来
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com