
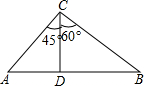
 如图,在△ABC中,CD⊥AB,∠ACD=45°,∠DCB=60°,AC=$40\sqrt{2}$,求AB.
如图,在△ABC中,CD⊥AB,∠ACD=45°,∠DCB=60°,AC=$40\sqrt{2}$,求AB. 分析 根据在△ABC中,CD⊥AB,∠ACD=45°,∠DCB=60°,AC=$40\sqrt{2}$,可以求得∠CDA=∠CDB=90°,从而可以求得各边的长,本题得以解决.
解答 解:∵在△ABC中,CD⊥AB,∠ACD=45°,∠DCB=60°,
∴∠CDA=∠CDB=90°,∠CAD=45°,∠B=30°,
∴CD=AD,BC=2CD,
∵AC=$40\sqrt{2}$,CD2+AD2=AC2,
∴CD=AD=$\sqrt{\frac{A{C}^{2}}{2}}=\sqrt{\frac{(40\sqrt{2})^{2}}{2}}$=40,
∴BC=80,
∴BD=$\sqrt{B{C}^{2}-C{D}^{2}}=\sqrt{8{0}^{2}-4{0}^{2}}=40\sqrt{3}$,
∴AB=AD+BD=40+40$\sqrt{3}$,
即AB的长是40+40$\sqrt{3}$.
点评 本题考查解直角三角形,解题的关键是明确各边之间的关系,由题目中的信息求出各边的长,然后找出所求问题需要的条件.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 14 | 4 | -2 | -4 | -2 | 4 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 任意打开一本200页的数学书,恰好是第50页 | |
| B. | 打开电视机,任选一个频道,正在播放足球赛 | |
| C. | 在空旷的操场上向上抛出的篮球一定会下落 | |
| D. | 阴天一定会下雨 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com