
 如图,P是y轴上一动点,是否存在平行于y轴的直线x=t,使它与直线y=x和直线y=-
如图,P是y轴上一动点,是否存在平行于y轴的直线x=t,使它与直线y=x和直线y=- x+2分别交于点D、E(E在D的上方),且△PDE为等腰直角三角形?若存在,求t的值及点P的坐标;若不存在,请说明原因.
x+2分别交于点D、E(E在D的上方),且△PDE为等腰直角三角形?若存在,求t的值及点P的坐标;若不存在,请说明原因. x+2=-
x+2=- t+2.
t+2.
 t+2),D点坐标为(t,t).
t+2),D点坐标为(t,t). t+2-t=-
t+2-t=- t+2,且t<
t+2,且t< .
. t+2=t,
t+2=t, ,-
,- t+2=
t+2= ,
, ).
). t+2=t,
t+2=t, ,
, ).
). t+2=2t
t+2=2t ,DE的中点坐标为(t,
,DE的中点坐标为(t, t+1),
t+1), ).
). t+2=-t,t=4>0(不符合题意,舍去),
t+2=-t,t=4>0(不符合题意,舍去), t+2=-2t,
t+2=-2t, t+1=0,
t+1=0, 时,△PDE为等腰直角三角形,此时P点坐标为(0,
时,△PDE为等腰直角三角形,此时P点坐标为(0, )或(0,
)或(0, );
); 时,△PDE为等腰直角三角形,此时P点坐标为(0,
时,△PDE为等腰直角三角形,此时P点坐标为(0, );
); x+2交y轴于点A,交直线y=x于点B,过B点作BM垂直于y轴,垂足为M,交DE于点N.
x+2交y轴于点A,交直线y=x于点B,过B点作BM垂直于y轴,垂足为M,交DE于点N.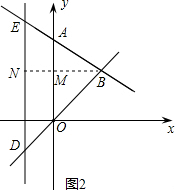
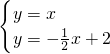 ,
, ,y=
,y= ,
, ,
, ),
), ,
, x+2=2,
x+2=2, =
= .
. =
= ,
,
 时,y=-
时,y=- x+2=
x+2= ,y=x=
,y=x=
 )或(0,
)或(0, ).
). =
=
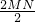 =
=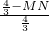 ,
, ,DE中点的纵坐标为
,DE中点的纵坐标为 t+1=
t+1= ,
, )
) =
=
 =
=
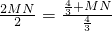 ,
, t+1=0,
t+1=0, 时,△PDE为等腰直角三角形,此时P点坐标为(0,
时,△PDE为等腰直角三角形,此时P点坐标为(0, )或(0,
)或(0, );
); 时,△PDE为等腰直角三角形,此时P点坐标为(0,
时,△PDE为等腰直角三角形,此时P点坐标为(0, );当t=-4时,
);当t=-4时,

科目:初中数学 来源: 题型:
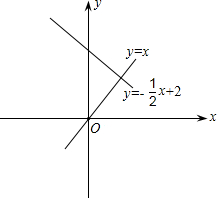 如图,P是y轴上一动点,是否存在平行于y轴的直线x=t,使它与直线y=x和直线y=-
如图,P是y轴上一动点,是否存在平行于y轴的直线x=t,使它与直线y=x和直线y=-| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源:2011-2012学年四川省资阳市安岳县自治乡九义校九年级(上)期末数学试卷(解析版) 题型:解答题
 x+2分别交于点D、E(E在D的上方),且△PDE为等腰直角三角形?若存在,求t的值及点P的坐标;若不存在,请说明原因.
x+2分别交于点D、E(E在D的上方),且△PDE为等腰直角三角形?若存在,求t的值及点P的坐标;若不存在,请说明原因.
查看答案和解析>>
科目:初中数学 来源:2011年黄冈教育阳江培训中心中考数学模拟试卷(16)(解析版) 题型:解答题
 x+2分别交于点D、E(E在D的上方),且△PDE为等腰直角三角形?若存在,求t的值及点P的坐标;若不存在,请说明原因.
x+2分别交于点D、E(E在D的上方),且△PDE为等腰直角三角形?若存在,求t的值及点P的坐标;若不存在,请说明原因.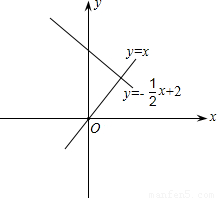
查看答案和解析>>
科目:初中数学 来源:2005年全国中考数学试题汇编《一次函数》(05)(解析版) 题型:解答题
 x+2分别交于点D、E(E在D的上方),且△PDE为等腰直角三角形?若存在,求t的值及点P的坐标;若不存在,请说明原因.
x+2分别交于点D、E(E在D的上方),且△PDE为等腰直角三角形?若存在,求t的值及点P的坐标;若不存在,请说明原因.
查看答案和解析>>
科目:初中数学 来源:2005年辽宁省大连市中考数学试卷(课标卷)(解析版) 题型:解答题
 x+2分别交于点D、E(E在D的上方),且△PDE为等腰直角三角形?若存在,求t的值及点P的坐标;若不存在,请说明原因.
x+2分别交于点D、E(E在D的上方),且△PDE为等腰直角三角形?若存在,求t的值及点P的坐标;若不存在,请说明原因.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com