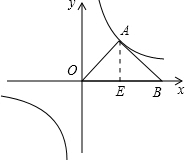
解:(1)过点A作AE⊥OB于E.
∵点A在y=x上,
∴∠AOB=45°,
∵∠OAB=90°,
∴∠OBA=45°,∠AOB=∠OBA,
∴OA=BA,
∴△OAB为等腰直角三角形.
∵AE⊥OB,
∴AE=OE=

OB=2,
∴A(2,2).
设双曲线的解析式为

,
∵点A在双曲线上,
∴
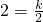
,
解得k=4.
∴双曲线的解析式为:

.
设直线AB的解析式为y
1=k
1x+b,由题意,得
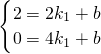
,
解得:
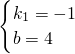
.
设直线AB的解析式为y
1=-x
1+4.
(2)设点G的纵坐标为a,则G(

,a),
∴
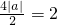
,
a=±1,
∴G(4,1)或G(-4,-1);
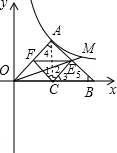
(3)连接AC,
∵△AOB是等腰直角三角形,
∴∠4=∠5=45°,AC⊥OB,
∴∠ACB=∠3+∠2=90°OC=BC=AC,
∵∠ECF=∠1+∠2=90°,
∴∠1=∠3,
∴△CFA≌△CEB.
∴AF=BE.
同理可得△CFO≌△CEA.
得AE=OF.
在Rt△AFE中,由勾股定理得
AF
2+AE
2=EF
2,
∴BE
2+OF
2=EF
2∴
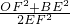
=

.
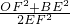
是定值为

.
分析:(1)要求直线AB和双曲线的解析式,就必须知道点A的坐标,求点A的坐标是关键,利用点A在y=x上及∠OAB=90°在这个等腰直角三角形中可以求出点A的坐标而解析式.
(2)要求双曲线上的点G的坐标,设点G的纵坐标为a,则G(

,a),然后代入面积公式就可以求出a的值,从而求出G的坐标.
(3)要确定
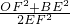
的值是否变化,就联想到把这三条线段转化到直角三角形中,利用勾股定理来确定这个式子的值,这就涉及到线段的转化,考虑到利用三角形全等,而在等腰直角三角形中作底边上的高或中线或顶角的角平分线这是常用的辅助线的作法,所以只要连接AC,问题就可以得到解决了.
点评:本题考查了反比例函数、一次函数的解析式、三角形全等、特殊图形辅助线的运用,学生在解答时要认真审题.找到解决问题的突破口.

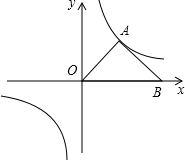
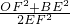 的值是否变化?若不变化请求出它的值,写出求解过程;若变化,说明理由.
的值是否变化?若不变化请求出它的值,写出求解过程;若变化,说明理由.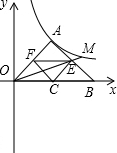
 解:(1)过点A作AE⊥OB于E.
解:(1)过点A作AE⊥OB于E. OB=2,
OB=2, ,
,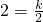 ,
, .
.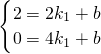 ,
,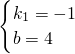 .
. ,a),
,a),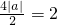 ,
,
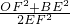 =
= .
.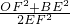 是定值为
是定值为 .
. ,a),然后代入面积公式就可以求出a的值,从而求出G的坐标.
,a),然后代入面积公式就可以求出a的值,从而求出G的坐标.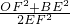 的值是否变化,就联想到把这三条线段转化到直角三角形中,利用勾股定理来确定这个式子的值,这就涉及到线段的转化,考虑到利用三角形全等,而在等腰直角三角形中作底边上的高或中线或顶角的角平分线这是常用的辅助线的作法,所以只要连接AC,问题就可以得到解决了.
的值是否变化,就联想到把这三条线段转化到直角三角形中,利用勾股定理来确定这个式子的值,这就涉及到线段的转化,考虑到利用三角形全等,而在等腰直角三角形中作底边上的高或中线或顶角的角平分线这是常用的辅助线的作法,所以只要连接AC,问题就可以得到解决了.

 黄冈创优卷系列答案
黄冈创优卷系列答案 8、如图,过点P画出射线PM,PN,使PM∥OA,PN∥OB,且射线PM和射线OA,射线PN和射线OB方向分别相同,量一量∠O和∠P,你能得到什么结论?如果射线PM和射线OA,射线PN和射线OB一组方向相同、另一组方向相反,∠O和∠P又有什么关系呢?如果两组方向都相反,∠O和∠P有什么关系?
8、如图,过点P画出射线PM,PN,使PM∥OA,PN∥OB,且射线PM和射线OA,射线PN和射线OB方向分别相同,量一量∠O和∠P,你能得到什么结论?如果射线PM和射线OA,射线PN和射线OB一组方向相同、另一组方向相反,∠O和∠P又有什么关系呢?如果两组方向都相反,∠O和∠P有什么关系?
 如图,过点O、A(1,0)、B(0,
如图,过点O、A(1,0)、B(0, 如图,过点P(2,
如图,过点P(2, 如图,过点A(1,0)的直线与y轴平行,且分别与正比例函数y=k1x,y=k2x和反比例y=
如图,过点A(1,0)的直线与y轴平行,且分别与正比例函数y=k1x,y=k2x和反比例y=