
【题目】已知,点P是Rt△ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.
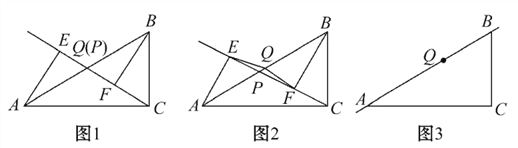
(1)如图1,当点P与点Q重合时,AE与BF的位置关系是________,QE与QF的数量关系是________.
(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明.
(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.
【答案】(1)AE∥BF,QE=QF;(2)QE=QF;(3)仍然成立
【解析】试题分析:(1)根据AAS推出△AEQ≌△BFQ,推出AE=BF即可;
(2)延长EQ交BF于D,求出△AEQ≌△BDQ,根据全等三角形的性质得出EQ=QD,根据直角三角形斜边上中点性质得出即可;
(3)延长EQ交FB于D,求出△AEQ≌△BDQ,根据全等三角形的性质得出EQ=QD,根据直角三角形斜边上中点性质得出即可.
试题解析:解:(1)如图1,当点P与点Q重合时,AE与BF的位置关系是AE∥BF,QE与QF的数量关系是AE=BF,理由是:∵Q为AB的中点,∴AQ=BQ,∵AE⊥CQ,BF⊥CQ,∴AE∥BF,∠AEQ=∠BFQ=90°,在△AEQ和△BFQ中,∵∠AQE=∠BQF,∠AEQ=∠BFQ,AQ=BQ,∴△AEQ≌△BFQ,∴QE=QF,故答案为:AE∥BF,QE=QF;
(2)QE=QF,证明:如图2,延长EQ交BF于D,∵由(1)知:AE∥BF,∴∠AEQ=∠BDQ,在△AEQ和△BDQ中,∵∠AQE=∠BQF,∠AEQ=∠BFQ,AQ=BQ,∴△AEQ≌△BDQ,∴EQ=DQ,∵∠BFE=90°,∴QE=QF;


(3)当点P在线段BA(或AB)的延长线上时,此时(2)中的结论成立.
证明:如图3,延长EQ交FB于D,如图3,
∵由(1)知:AE∥BF,∴∠AEQ=∠BDQ,在△AEQ和△BDQ中,∵∠AQE=∠BQF,∠AEQ=∠BFQ,AQ=BQ,
∴△AEQ≌△BDQ,∴EQ=DQ,∵∠BFE=90°,∴QE=QF.



 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】某市为鼓励居民节约用水,对自来水用户按分段计费方式收取水费:若每月用水不超过10m3,则按每立方米1.5元收费;若每月用水超过10m3,则超过部分按每立方米3元收费,如果某居民户今去年12月份缴纳了36元水费,那么这户居民去年12月份的实际用水量为( )
A. 7m3B. 12m3C. 17m3D. 24m3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为x=2的抛物线y= ![]() 反比例函数
反比例函数![]() (x>0)交于点B,过点B作x轴的平行线,交y轴于点C,交反比例函数
(x>0)交于点B,过点B作x轴的平行线,交y轴于点C,交反比例函数![]() 于点D,连接OB、OD。则下列结论中:①ab>0;②方程
于点D,连接OB、OD。则下列结论中:①ab>0;②方程![]() 的两根为0,4;③3a+b<0;④tan∠BOC=4tan∠COD正确的有
的两根为0,4;③3a+b<0;④tan∠BOC=4tan∠COD正确的有

A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于点C.抛物线
与x轴交于点A,与y轴交于点C.抛物线![]() 经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
经过A,C两点,且与x轴交于另一点B(点B在点A右侧).

(1)求抛物线的解析式及点B坐标;
(2)若点M是线段BC上的一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;
(3)试探究当ME取最大值时,在抛物线上、x轴下方是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校将举办一场“中国汉字听写大赛”,要求各班推选一名同学参加比赛,为此,初四某班组织了五轮班级选拔赛,在这五轮选拔赛中,甲、乙两位同学的平均分都是96分,甲的成绩的方差是1,乙的成绩的方差是0.8.根据以上数据,下列说法正确的是( )
A.甲的成绩比乙的成绩稳定
B.乙的成绩比甲的成绩稳定
C.甲、乙两人的成绩一样稳定
D.无法确定甲、乙的成绩谁更稳定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com