
分析 (1)连接AC、BC,先根据等弧得:∠AEC=∠BAE,则∠CAB=2∠BAE,再由直径所对的圆周角为直角得:∠ACB=90°,直角三角形的两锐角互余得:∠CAB+∠CBA=90°,等量代换可得结论;
(2)如图2,连接EO设∠OEA=∠OAE=α,证明∠GFE=∠GEF=90°-α,则GE=GF;
(3)如图3,作辅助线,构建直角三角形,证明∠COM=∠BOM则OM⊥BC,由(2)得∠GEM=90°,则CM∥EG,CF=CN=6,设MN=x,则CM=BM=6+x,根据三角函数得:cos∠EBM=$\frac{MB}{EB}=\frac{EB}{BN}$,列式求得x的值,在△OBM中,设OM=m,则OE=OB=m+4,根据勾股定理列方程可得结论.
解答 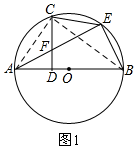 证明:(1)连接AC、BC,
证明:(1)连接AC、BC,
∴∠CEA=∠CBA,
∵E为$\widehat{BC}$的中点,
∴$\widehat{BE}$=$\widehat{CE}$,
∴∠CAE=∠BAE,
∴∠CAB=2∠BAE,
∵AB是直径,
∴∠ACB=90°,
∴∠CAB+∠CBA=90°,
∴2∠BAE+∠AEC=90°,
∴∠AEC=90°-2∠BAE;
(2)连接EO,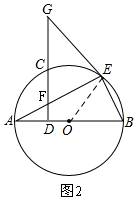
∵OA=OE,
∴∠OEA=∠OAE,
设∠OEA=∠OAE=α,
∵EG为切线,
∴OE⊥EG,
∴∠OEG=90°,
∴∠GEA=90°-∠AEO=90°-α,
∵DG⊥AB,
∴∠FDA=90°,
∴∠FAD+∠AFD=90°,
∴∠AFD=90°-α=∠GFE,
∴∠GFE=∠GEF=90°-α,
∴GE=GF;
(3)如图3,连接CE、CB、OE、OC,CB与AE交于点N,CB与OE交于点M,
∵E为$\widehat{BC}$的中点,
∴∠COM=∠BOM,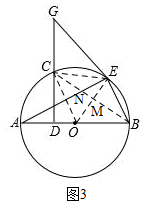
∵OC=OB,
∴OM⊥BC,
∴∠OMB=90°,
由(2)得∠GEM=90°,
∴CM∥EG,
∴∠GEF=∠CNF,
∵∠GFE=∠GEF,
∴∠CFE=∠CNF,
∴CF=CN=6,
设MN=x,则CM=BM=6+x,
cos∠EBM=$\frac{MB}{EB}=\frac{EB}{BN}$,
∴$\frac{6+x}{4\sqrt{5}}$=$\frac{4\sqrt{5}}{6+2x}$,
解得:x1=2,x2=-11(舍),
MB=6+x=6+2=8,
由勾股定理得:ME=$\sqrt{B{E}^{2}-B{M}^{2}}$=$\sqrt{(4\sqrt{5})^{2}-{8}^{2}}$=4,
在△OBM中,设OM=m,则OE=OB=m+4,
OM2+MB2=OB2,
即m2+82=(m+4)2,
∴OM=m=6,
∴OE=OB=6+4=10.
则⊙O的半径为10.
点评 本题是圆的综合题,考查了圆的切线的性质、勾股定理、三角函数、圆周角定理、垂径定理等知识,在圆中求线段的长常利用三角函数或勾股定理列等式求解,本题也是如此,第三问设未知数列方程是关键.


科目:初中数学 来源:2017届辽宁省九年级3月月考数学试卷(解析版) 题型:选择题
如图,在直角坐标系中,⊙O的半径为1,则直线y=﹣x+ 与⊙O的位置关系是( ).
与⊙O的位置关系是( ).
A.相离 B.相交 C.相切 D.以上三种情形都有可能

查看答案和解析>>
科目:初中数学 来源:2016-2017学年贵州省七年级下学期第一次月考数学试卷(解析版) 题型:单选题
某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( )
A. 第一次左拐30°,第二次右拐30°
B. 第一次右拐50°,第二次左拐130°
C. 第一次右拐50°,第二次右拐130°
D. 第一次向左拐50°,第二次向左拐120°
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
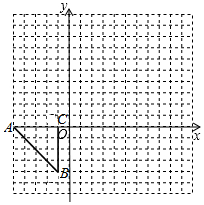 如图,直角坐标系中的△ABC的三个顶点分别为A(-5,0),B(-1,-4),C(-1,0).
如图,直角坐标系中的△ABC的三个顶点分别为A(-5,0),B(-1,-4),C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
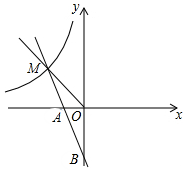 如图,一次函数y=kx+b的图象经过A(-1,0),B(0,-2)l两点,与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第二象限交于点M,△OBM的面积是3.
如图,一次函数y=kx+b的图象经过A(-1,0),B(0,-2)l两点,与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第二象限交于点M,△OBM的面积是3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
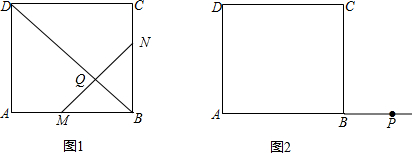
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
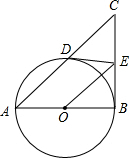 如图,AB为⊙O的直径,E是⊙O外一点,过点E作⊙O的两条切线ED、EB,切点分别为点D,B,连接AD并延长交BE延长线于点C,连接OE.
如图,AB为⊙O的直径,E是⊙O外一点,过点E作⊙O的两条切线ED、EB,切点分别为点D,B,连接AD并延长交BE延长线于点C,连接OE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
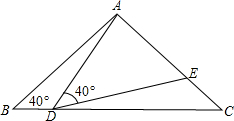 如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com