
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
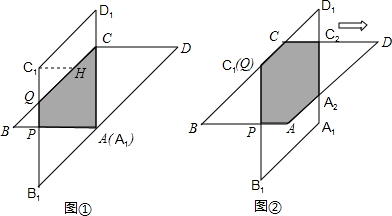 解:(1)∵由条件可知△ABC和△ADC都是等腰直角三角形,
解:(1)∵由条件可知△ABC和△ADC都是等腰直角三角形,| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
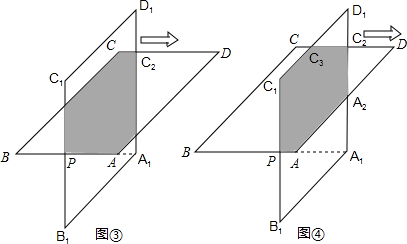 ①若0≤x≤8
①若0≤x≤8| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| b |
| 2a |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |


科目:初中数学 来源: 题型:
| k |
| x |
 0)的图象相交于P、Q两点,过点P作PB⊥x轴于点B.已知tan∠PAB=
0)的图象相交于P、Q两点,过点P作PB⊥x轴于点B.已知tan∠PAB=| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•北碚区模拟)已知:如图,在梯形ABCD中,AB∥CD,AD=BC,AB=10,CD=18,∠ADC=60°,过BC上一点E作直线EH,交CD于点F,交AD的延长线于点H,且EF=FH.
(2012•北碚区模拟)已知:如图,在梯形ABCD中,AB∥CD,AD=BC,AB=10,CD=18,∠ADC=60°,过BC上一点E作直线EH,交CD于点F,交AD的延长线于点H,且EF=FH.查看答案和解析>>
科目:初中数学 来源: 题型:
 该厂7月份进货量在6月份的基础上增加2a%.若要使7月份进货金额为5130400元,请你估算出a的最大整数值.
该厂7月份进货量在6月份的基础上增加2a%.若要使7月份进货金额为5130400元,请你估算出a的最大整数值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com