解:(1)证明:∵正方形ABCD,
∴∠DAB=∠DCB=90°,AD=DC,
∴∠DCF=90°=∠DAE,
∵CF=AE,
∴△ADE≌△CDF.
(2)证明:∵正方形ABCD,
∴AB=BC=AD,∠DAB=∠B=90°,
∵E为AB中点,H为BC的中点,
∴AE=BH,
∴△DAE≌△ABH,
∴∠EDA=∠BAH,
∵∠AED+∠ADE=90°,
∴∠AED+∠BAH=90°,
∴∠AGE=180°-90°=90°,
∴AH⊥ED.
∵E是AB的中点,
∴AE=

AB.
∵正方形ABCD的边长是2,
∴AD=AB=2,
∴AE=1.
在△EAD中,由勾股定理得:DE=
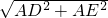
=

=

,
由三角形的面积公式得:

AE×AD=

DE×AG,
∴

×1×2=

×

AG,
∴AG=

分析:(1)根据正方形的性质推出∠DAB=∠DCB=90°,AD=DC,根据SAS即可证出答案;
(2)根据正方形的性质推出AE=BH,根据SAS证△DAE≌△ABH,推出∠EDA=∠BAH,求出∠AED+∠BAH=90°,根据三角形的内角和定理求出∠AGE,再根据三角形的面积公式表示出△EAD的面积即

AE•AD或

ED•AG,由已知数据即可求出AG的长.
点评:题主要考查对三角形的面积,正方形的性质,全等三角形的性质和判定,三角形的内角和定理,勾股定理,垂线等知识点的理解和掌握,能综合运用这些性质进行推理是解此题的关键.

 如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE.
如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE. AB.
AB.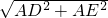 =
= =
= ,
, AE×AD=
AE×AD= DE×AG,
DE×AG, ×1×2=
×1×2= ×
× AG,
AG,
 AE•AD或
AE•AD或 ED•AG,由已知数据即可求出AG的长.
ED•AG,由已知数据即可求出AG的长.

 (2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
(2013•北碚区模拟)如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点. 如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上.
如图,已知正方形ABCD,点E在BC边上,将△DCE绕某点G旋转得到△CBF,点F恰好在AB边上. 如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.
如图,已知正方形ABCD的对角线AC,BD相交于点O,E是AC上的一点,过点A作AG⊥BE,垂足为G,AG交BD于点F.