
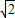
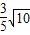
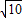 ,再利用面积法得到
,再利用面积法得到 BH•DC=
BH•DC= BC•DE,可计算出DE=
BC•DE,可计算出DE=
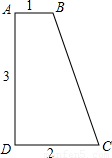
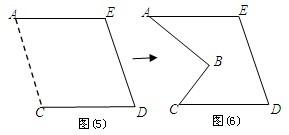
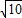 ,若将直角梯形ABCD木板从一个圆钢圈中穿过,这个圆钢圈的最小直径为DE.
,若将直角梯形ABCD木板从一个圆钢圈中穿过,这个圆钢圈的最小直径为DE.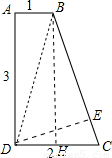 BH⊥DC于H,DE⊥BC于E,连BD,
BH⊥DC于H,DE⊥BC于E,连BD,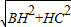 =
=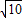 ,
, BH•DC=
BH•DC= BC•DE,
BC•DE,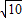 DE=3×2,
DE=3×2,
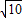 ,
,
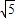 <2,
<2,

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:044
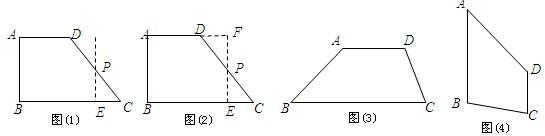
(1)野营活动中,小明用一张等腰三角形的铁皮代替锅,烙一块与铁皮形状、大小相同的饼.烙好一面后把饼翻身,这块饼仍能正好落在“锅”中.这是为什么?
(2)小丽用如图①的直角三角形铁皮,烙一块与铁皮形状、大小相同的饼.如果烙好一面后就把饼翻身,那么这块饼不能正好落在“锅”中.如图②,小丽将饼切了一刀,然后将两小块翻身,结果饼就能正好落在“锅”中.这又是为什么?
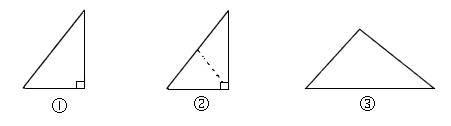
(3)如果用来烙饼的铁皮既不是等腰三角形也不是直角三角形(如图③),那么烙好一面后,怎样将烙饼翻身,才能使烙饼仍能正好落在“锅”中?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com