
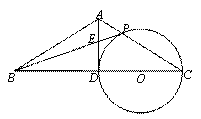
已知:如图,在△ABC中,AB=AC,点D是边BC的中点.以
CD为直径作⊙O,交边AC于点P,连接BP,交AD于点E.
(1)求证:AD是⊙O的切线;
(2)如果PB是⊙O的切线,BC=4,求PE的长.
科目:初中数学 来源: 题型:
定义1:在 中,若顶点
中,若顶点 ,
,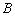 ,
, 按逆时针方向排列,则规定它的面积为“有向面积”;若顶点
按逆时针方向排列,则规定它的面积为“有向面积”;若顶点
 ,
,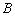 ,
, 按顺时针方向排列,则规定它的面积的相反数为
按顺时针方向排列,则规定它的面积的相反数为 的“有向面积”。“有
的“有向面积”。“有 向面积”用
向面积”用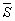 表示,
表示,


 例如图1中,
例如图1中,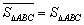 ,图2中,
,图2中,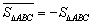 。
。
定义2:在平面内任取一个 和点
和点 (点
(点 不在
不在 的三边所在直线上),称有序数组(
的三边所在直线上),称有序数组( ,
,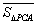 ,
, )为点
)为点 关于
关于 的“
的“ 面积坐标”,记作
面积坐标”,记作 ,例如图3中,菱形
,例如图3中,菱形 的边长为2,
的边长为2,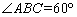 ,则
,则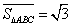 ,点
,点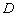 关于
关于 的“面积坐标”
的“面积坐标”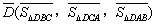 为
为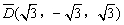 。
。
 在图3中,我们知道
在图3中,我们知道 ,利用“有向面积”,我们也可以把上式表示为:
,利用“有向面积”,我们也可以把上式表示为:
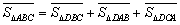 。
。
应用新知:
(1)如图4,正方形 的边长为1,则
的边长为1,则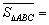 ,点
,点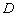 关于
关于 的“面积坐标”是 ;
的“面积坐标”是 ;
探究发现:
(2)在平面直角坐标系 中,点
中,点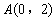 ,
,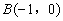 .
.
①若点 是第二象限内任意一点(不在直线
是第二象限内任意一点(不在直线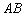 上),设点
上),设点 关于
关于 的“面积坐标”为
的“面积坐标”为 ,
,
试探究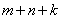 与
与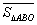 之间有怎样的数量关系,并说明理由;
之间有怎样的数量关系,并说明理由;
②若点 是第四象限内任意一点,请直接写出点
是第四象限内任意一点,请直接写出点 关于
关于 的“面积坐标”(用
的“面积坐标”(用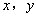 表示);
表示);
解决问题:
(3)在(2)的条件下,点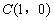 ,
, ,点
,点 在抛物线
在抛物线 上,求当
上,求当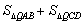 的值最小时,点
的值最小时,点 的横坐标。
的横坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,边长为1的正方形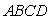 中有两个动点
中有两个动点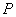 ,
, 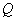 ,点
,点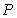 从点
从点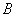 出发沿
出发沿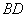 作匀速运动,到达点
作匀速运动,到达点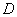 后停止;同时点
后停止;同时点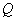 从点
从点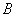 出发,沿折线
出发,沿折线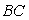 →
→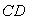 作匀速运动,
作匀速运动,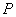 ,
,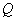 两个点的速度都为每秒1个单位,如果其中一点停止运动,则另一点也停止运动.设
两个点的速度都为每秒1个单位,如果其中一点停止运动,则另一点也停止运动.设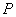 ,
,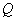 两点的运动时间为
两点的运动时间为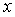 秒,两点之间的距离为
秒,两点之间的距离为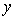 ,下列图象中,能表示
,下列图象中,能表示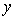 与
与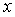 的函数关系的图象大致是
的函数关系的图象大致是 
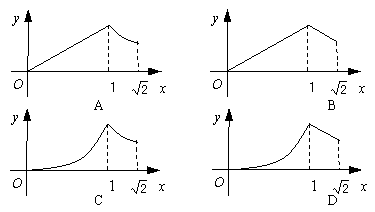

查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系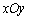 中,对于任意三点
中,对于任意三点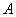 ,
,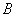 ,
,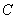 的“矩面积”,给出如下定义:
的“矩面积”,给出如下定义:
“水平底”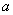 :任意两点横坐标差的最大值,“
:任意两点横坐标差的最大值,“ 铅垂高”
铅垂高”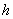 :任意两点纵坐标差的最大值,则“矩面积”
:任意两点纵坐标差的最大值,则“矩面积” .
.
例如:三点坐标分别为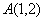 ,
,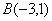 ,
,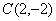 ,则“水平底”
,则“水平底”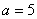 ,“铅垂高”
,“铅垂高”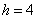 ,“矩面积”
,“矩面积”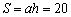 .
.
(1)已知点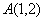 ,
,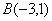 ,
,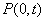 .
.
①若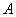 ,
,
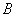 ,
,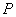 三点的“矩面积”为12,求点
三点的“矩面积”为12,求点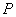 的坐标;
的坐标;
②直接写出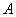 ,
,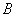 ,
,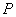 三点的“矩面积”的最小值.
三点的“矩面积”的最小值.
(2)已知点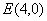 ,
,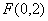 ,
,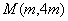 ,
,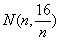 ,其中
,其中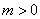 ,
,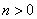 .
.
①若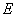 ,
,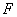 ,
,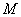 三点的“矩面积”为8,求
三点的“矩面积”为8,求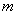 的取值范围;
的取值范围;
②直接写出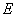 ,
,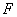 ,
,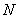 三点的“矩面积”的最小
三点的“矩面积”的最小 值及对应
值及对应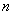 的
的 取值范围.
取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
课本上,公式 (a-b)2=a2-2ab+b2 是由公式 (a+b)2=a2+2ab+b2 推导得出的.
已知 (a+b)4=a4+4a3b+6a2b2+4ab3+b4,则 (a-b)4= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com