
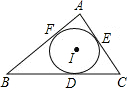
 在△ABC中,已知BC=a,CA=b,AB=c,s=
在△ABC中,已知BC=a,CA=b,AB=c,s= ,内切圆I和BC,CA,AB分别相切于点D,E,F.求证:
,内切圆I和BC,CA,AB分别相切于点D,E,F.求证: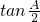 .
.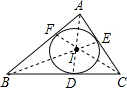 证明:(1)设AE=AF=x,BF=BD=y,CD=CE=z,
证明:(1)设AE=AF=x,BF=BD=y,CD=CE=z, ;
; ;
;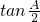 =(s-a)
=(s-a)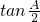
 rc+
rc+ ra+
ra+ rb
rb r(a+b+c)
r(a+b+c)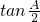 .
. (AB+AC-BC),再将s的式子代入上式即可证得本题所求的结论;
(AB+AC-BC),再将s的式子代入上式即可证得本题所求的结论; ,即(s-a)•tan
,即(s-a)•tan ;将△ABC分为△AIB、△AIC、△BIC三部分,分别用三角形ABC的三边长即⊙I的半径表示出它们的面积,进而由S△ABC=S△ABI+S△BCI+S△CAI得出所要证的结论.
;将△ABC分为△AIB、△AIC、△BIC三部分,分别用三角形ABC的三边长即⊙I的半径表示出它们的面积,进而由S△ABC=S△ABI+S△BCI+S△CAI得出所要证的结论.

科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com