Question

已知一个样本1，4，2，a，3，它的平均数是b，且a，b是方程x²-8x+15=0的两个根，求这个样本的方差．

Answer 1

解：∵x²-8x+15=0，
∴（x-5）（x-3）=0，
∴x=3或x=5，
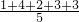
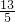
∵=≠5，
∴a=5，b=3，
∴方差=[（1-3）²+（4-3）²+（2-3）²+（5-3）²+（3-3）²]=2．
∴这个样本的方差是3．
分析：先求出方程的解，再根据1，4，2，a，3，它的平均数是b，求出a，b的值，最后根据方差公式进行计算即可．
点评：本题考查方差、平均数和一元二次方程的解：一般地设n个数据，x₁，x₂，…x_n的平均数为，则方差S²=[（x₁-）²+（x₂-）²+…+（x_n-）²]，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．