练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．国家统计局发布数据，2015上半年我国国内生产总值为296 868亿元，用科学记数法表示为（　　）
    A．0.296868×104B．2.96868×105C．2.96868×106D．29.6868×104

    分析 科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．

    解答 解：296 868亿元用科学记数法表示为2.96868×105，
    故选：B．

    点评 此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．如图，直线a∥b，∠3=85°，求∠1、∠2的度数，根据下面的解答过程，填空或填写理由．
    解：∵a∥b已知
    ∴∠1=∠4
    ∵∠4=∠3对顶角相等
    ∠3=85°已知
    ∴∠1=85°（等量代换）
    又∵∠2+∠3=180°
    ∴∠2=95°（等式的性质）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．学了全等三角形的判定后，小明编了这样一个题目：“已知：如图，AB=AC，AD=AE，∠AEC=∠ADB，求证：△ABD≌△ACE．”老师说他的已知条件给多了，那么可以去掉的一个已知条件是：∠AEC=∠ADB．去掉上述条件后，请你完成证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．解方程：
    （1）2（2x+1）-3（x-1）=12　　　
    （2）$\frac{x-3}{5}$-$\frac{x-4}{3}$=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

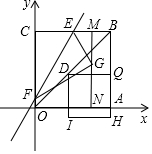    7．如图，四边形OABC是一张放在平面直角坐标中的正方形纸片，点O与坐标原点重合，点A 在x轴上，点C在y轴上，OC=4，点E为BC的中点，点N的坐标为（3，0），过点 N且平行于y轴的直线MN与EB交于点M．现将纸片折叠，使顶点C落在MN上，并与MN上的点G重合，折痕为EF，点F为折痕与y轴的交点．连接OB，D为OB上动点，作DQ∥x轴交BA于点Q，以DQ为边，向下作正方形DQHI，设点D的横坐标为t．
    （1）求点G的坐标及折痕EF所在直线的解析式．
    （2）点D从点O运动到点B的过程中，正方形DQHI与△OAB重叠的面积S与t的函数关系式，并求出自变量t的取值范围．
    （3）设点P为直线EF上的点，是否存在这样的点P，使得以P、F、G为顶点的三角形为等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．以下问题，不适合用全面调查的是（　　）
    A．了解全班同学每周体育锻炼的时间B．旅客上飞机前的安检
    C．了解全市中小学生每天的零花钱D．学校招聘教师，对应聘人员面试

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如果直线l：y=kx+b与曲线（包括折线、弧线、双曲线、抛物线等）有两个不同的交点我们把这两点间的线段的长度叫直线l与曲线的“非凡距离”
    （1）已知直线l：y=x+4与坐标轴相交于点A、B，坐标系原点为O，求直线l与折线AOB的非凡距离；
    （2）若直线l：y=2x+b与双曲线y=-$\frac{1}{x}$的非凡距离为$\sqrt{5}$，求b的值；
    （3）已知直线l：y=x-2与抛物线y=-x2+mx-1交于点P，Q，若抛物线与y轴相交于N点，⊙M恰好经过P、Q，当直线l与抛物线的非凡距离取最小值时，求点N到⊙M的圆心M的距离的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

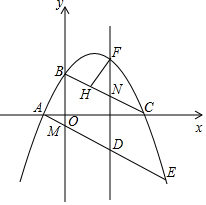    12．如图所示，在平面直角坐标系中，抛物线y=ax2+bx+2（a≠0）经过点B，与x轴交于点A，C（点A在点C的左侧），A（-1，0），C（4，0），连接AB，BC，点M（0，-$\frac{1}{2}$）为y轴负半轴上的一点，连接AM并延长交抛物线于点E，点D为线段AE上的一个动点，过点D作y轴的平行线与抛物线交于点F，与线段BC交于点N
    （1）求出抛物线的表达式及直线BC的表达式
    （2）在点D运动的过程中，点FN的值最大时，在线段BC上是否存在一点H，使得△FNH与△ABC相似，如果存在，求出此时H点的坐标
    （3）当DF=4时，连接DC，四边形ABCD先向上平移一定单位长度后，使点D落在x轴上，然后沿x轴向左平移n（1＜n＜4）个单位长度，用含n的表达式表示平移后的四边形与原四边形重叠部分的面积S（直接写出结果）

    查看答案和解析>>

    同步练习册答案